CCD PHOTOMETRY
E. Norman Walker
For some people there will come a time when obtaining pictures of the sky or astronomical objects will no longer be sufficiently satisfying. No matter how great the beauty of the images, or the sense of wonder and awe which they inspire in the viewer, some observes will find that there is an itch of inquisitiveness in the back of their brains which, when scratched, poses the question: "Is there more that I could do?" For CCD observers the answer is an unequivocal "Yes!" The nature of the CCD allows its ready use for both photometry, that is brightness measurements, astrometry, that is positional measurements and morphological studies, that is changes in the image structure such as the rotation and changes of a passing comet. In this chapter we will describe the principles and practice of photometry.
What is Photometry?
Photometry is literally the measurement of light, how much, what colour and so on. Astronomically it is generally thought of in terms of measuring the colours and brightness of stars but it also includes the investigation of surface brightness in extended objects such as the moon, the planets, galaxies and, for example, arcs of emission nebulosity in our own galaxy. The unit of brightness measurement, which is used on a regular basis by astronomers, is the ‘magnitude’. This has its origins at least as far back as the classical Greek, Hipparchus, about 120 BC. In their attempts to try to understand the nature of the natural world one of the things, which that culture had to do, was to describe the nature of the sky, that is the large-scale environment in which we find ourselves. In order to try to quantify their description of the night sky for both philosophical reasons, and practicalities such as navigation, they arbitrarily divided the apparent brightness of the naked eye stars into six categories or magnitudes. The brightest stars were assigned to category one, first magnitude and the faintest stars to category six, the sixth magnitude. In between the brightest and the faintest stars were stars of second magnitude, third magnitude and so on.
This situation persisted until well after the Renaissance and into our present era of quantitative scientific enquiry. Advances in technology in the nineteenth century allowed the more accurate measurement of light in the laboratory and it came to be realised that there was a factor of about 100 difference in the brightness of a first and sixth magnitude star. After some international discussion the system proposed by the English astronomer, Norman Pogson, was adopted. This defined one magnitude as the fifth root of 100, i.e. 2× 512, and thus placed the ancient Greek system into a quantitative, modern system. (Note that this means that the system of magnitudes is logarithmic, with a base of 2× 512 rather than the more familiar 10. This has its origins in the response of human beings to external stimuli. Andrew T Young, California based photometry guru has ably pointed out that, in fact, human sensory responses follow power laws with different exponents for different senses. However, over the last 100 years or so, as scientists have struggled to put subjective human responses onto scientifically measured scales, logarithms have been used and we now have the logarithmic scales of magnitudes in astronomy, decibels in the measurement of sound, the chromatic and diatonic scales in musical notation etc). Thus a second magnitude star is ~2.5 times brighter than a third magnitude star and a first magnitude star is ~6× 25 (2× 5 x 2× 5) brighter than a third magnitude star and so on. The difference in magnitude between two stars is generally referred to as a D mag. where D is the Greek symbol, delta, commonly used in scientific notation to represent the difference between two values. Using your CCD to determine stellar brightnesses will almost always result in a list of D magnitudes between the various stars measured from one exposure.
Note that all the magnitudes that are being referred to at the moment are known as apparent magnitudes, that is the magnitude that stars appear to have when observed from the Earth. Astronomers also use absolute magnitudes, which is the true, intrinsic brightness of a star. The zero point of this is adjusted to the brightness which stars would appear to have to us on Earth if they were all at a common distance of 10 parsecs (32× 6 light years). Therefore, although the CCD is a linear detector, that is it produces double the signal if the light is doubled and ten times the signal if ten times as much light is input, it is common practice to convert these linear measures to the logarithmic scale of magnitudes so that the result can be compared with those based upon the historical system.
Technology and instrumentation moved on and the potential accuracy of brightness measurements increased. With the start of the use of photography in astronomy, and later photomultiplier tubes, it soon became clear that it was no longer adequate to say that a star had a certain magnitude but it was necessary to say in what colour that magnitude was measured. The sensitivity of the photographic emulsion is such that it records light of a blue colour more readily than does the human eye. A pair of stars, which seemed to be of the same brightness of the human eye, might seem to have very different brightnesses when recorded on a photographic plate. This led to the development of the use of filters in astronomical photometry. In their simplest form these arc coloured pieces of glass, which allow a restricted range of colours to pass. When such filters are used then it is possible to say, for example, that a star has a certain magnitude in the blue, another magnitude in the visual, and the difference between these two magnitudes, the blue minus the visual (B-V) tells us something about the colour of the star and hence its temperature. We will return to the subject of filters and their use with CCDs below.
In case it is thought that the measurement of stellar brightness is an uninteresting niche in the panoply of astronomical techniques we should pause for a moment to consider how much of our current understanding of the universe is due to this technique. The measurement of brightness changes in eclipsing spectroscopic binary stars allows us to calculate the true dimensions of stars other than our Sun. Brightness changes in RR Lyra stars allow us to measure distances within our own galaxy while brightness changes in Cepheid variables allows us to do the same for distant galaxies. The detection of supernova explosions shows us the way in which some stars die and the time scale of brightness changes in quasars puts limits on the sizes of some of the brightest objects in the universe. The slow variations in some long period variables shows us how some stars behave as they approach old age while the rapid variations in yet other stars allows us to probe the internal structure of these stars. It is no exaggeration to state that there is almost no aspect of our current understanding of the universe that has not been fundamentally influenced by the measurement of brightness and brightness changes. The use of your CCD for this purpose allows you to progress from the acquisition of images of the sky to the world of contributing new knowledge to add to humanity’s understanding of the natural world. It is one of the wonders of the CCD that it can allow you to do both and it is up to you to decide how you wish to use it.
The Effect of the Earth’s Atmosphere
Even if you have never thought about it quantitatively, you cannot fail to be qualitatively aware that the Earth’s atmosphere absorbs light. You know that the daytime sky is blue, that even on apparently cloud free days the Sun or the stars are sometimes brighter than at other times. You also know that when the Sun is low in the sky it appears fainter and redder than when it is high in the sky. All these effects are due to that complex mix of gasses and particles which we call the atmosphere, and without which the Earth would be a lifeless ball of rock. The blue of the daytime sky is due to the fact that many of the molecules which make up the atmosphere have the same size as the wavelength of blue light, about half of one micron. This causes them to scatter the blue light, hence the blue sky, while the longer wavelength of red light, about 0× 7 of a micron, allows it to pass through the atmosphere less effected, hence the red of the setting sun. Note however, that the Sun is not only redder but also much fainter when near the horizon. This is due to the fact that there is much more atmosphere for the light to pass through at low elevations. Light of all colours is being absorbed but the red light is being affected less than the blue light.
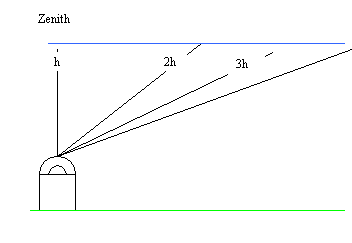
Thus there are two effects. One is the amount of atmosphere the light has to travel through and the other is the differential effect that the atmosphere has on different colours. It is possible to calculate or measure the amount of these effects. First we make the simplifying assumption that the surface of the Earth is flat and the atmosphere is a uniform layer above the Earth's surface. Then the length of the light path through the atmosphere varies as the secant of the angle of the object from the observer's zenith. This is normally written as sec Z, (secant is 1/cosine). The cartoon in figure 1 shows the effect.

Figure 1 shows the effect of observing at increasing angles from the zenith upon the path length of the light through the Earth's atmosphere.
If we call the height of the atmosphere at the zenith 'h' then at Z = 60° the atmospheric distance is 2h. Table 1 below shows how quickly the atmospheric path length increases as one observes more than 60° from the zenith. One degree above the horizon there is 100 times more atmosphere to look through than at the zenith. No wonder that the Sun looks fainter. The path length through the atmosphere is also known as the 'air mass'.
Table 1
|
Zenith Distance |
Sec Z |
|
0° |
1 |
|
60° |
2 |
|
70° |
3 |
|
75° |
4 |
|
78° |
5 |
|
84° |
10 |
|
89° |
100 |
Note that this does not mean that there is no absorption at the zenith; just that this is where it is at a minimum. The amount of absorption at the zenith will depend upon the height of the observatory above sea level, the quality of the local sky and many other factors. One thing is certain. There will be much more absorption for the ultra violet and blue wavelengths than there will be for the red and infra-red wavelengths.
Figure 2 below shows the amount of this effect graphically.
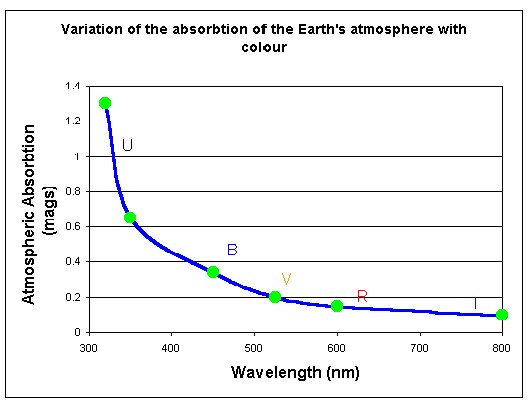
Figure 2 shows the difference in atmospheric absorption at different wavelengths at a good site.
In magnitudes the approximate values at different colours under good sky conditions are: -
0× 2 mag. times the air mass for the V band
0× 334 - 0× 03(B-V) mag. times the air mass for the B band and,
0× 65 - 0× 03(B-V) mag. times the air mass for the U band.
Note the important fact that for accurate work a correction, which is a function of the colour of the star, must also be incorporated. The reason for this is easy to understand and is relevant to our discussion below concerning filters. The width of all of the U, B, V, R and I filters is sufficient that the energy curve of the stars can show a significant gradient across the filter's passband. A red (cool) star will have more energy in the red half of the filter in proportion to a blue (hot) star. This has the effect of changing the 'centre of gravity' of the filter to the red or blue, hence the need to apply a correction which depends upon the colour (temperature) of the star.
The small size of a typical CCD means that a very limited range of zenith distances will be contained on one frame unless one is using the device with a wide angle lens. Thus under certain circumstances it would be thought that the colour corrections might be ignored. However, suppose that one wants to compare results of the same field taken over a wide range of zenith distances. In that case, these corrections will be ignored at your peril. It should also be noted that the above values are approximate and will not only vary from site to site but will also depend upon what type of optical system is being used to make the observations. An all reflecting system will have less UV absorption than a conventional refractor. A Schmidt-Cassegrain with a non UV transmitting focal reducer will have different values to the same telescope with no focal reducer. These corrections have to be determined empirically for every telescope/CCD combination and if you change your system by the inclusion or removal of an extra lens then you will have to re-determine these values. The good news is that it is not difficult, and once it has been done it is likely that the corrections will be constant for years. Later we will tell you how to determine these corrections. This now leads us to one of the most important aspects of how to use a CCD if scientifically useful photometry is to be produced.
Filters and why you should use them
It is one of the great strengths of the CCD that it is sensitive to a very wide range of colours. The human eye is sensitive to colours that range from about 0.4 microns in the blue to about 0× 7 microns in the red. CCDs aimed at the amateur market are now available whose sensitivities extend from well to the ultra violet of 0× 4 microns, and hence near to the atmospheric limit at about 0× 32 microns, to about 1 micron, or beyond, which is well into the near infra red. If we try to do photometry without a filter what will happen? Suppose that you take an unfiltered exposure, near to the zenith, of a stellar field which contains a very red and a very blue star. The magnitudes that you get might well not agree with any published values, even naked eye ones, as the spectral response of the CCD is not like that of any of the earlier detectors. However, that is not the worst part of the situation. Imagine now that you take a second exposure with the same telescope/CCD combination for the same field but this time at a zenith distance of 60°, sec Z = 2. Look back now at figure 2. It is clear that the UV light of the stars will have been reduced by perhaps 70% while the V light of the stars will have been reduced by the much smaller amount of about 30%. The red and infra-red light will have been reduced by an even smaller amount. At this stage it is clear that the bluer of the two stars will have been dimmed by a much larger amount than the redder of the pair.
Let us now put this into a practical example of a CCD observer wanting to monitor the decaying light curve of a supernova. When a supernova explodes there is an immediate pulse of high energy particles in the region of gamma rays and the far ultra violet. With time the cloud of material which was ejected at the time of the explosion, expands and cools. Whereas, at the start, almost all the energy was emitted in the far ultra violet, slowly the peak of the energy emission moves redwards. First it will move into the blue band then the visual, later it will move to the red and then the infra-red. Your CCD can detect all these colours, albeit with varying degrees of sensitivity. We have already shown above that the magnitude difference between a red and a blue star will vary as zenith distance.
What do you think will happen to the magnitude difference that you measure between your comparison stars and the varying colour of the supernova over several months as you observe at different zenith distances? One of the very strengths of the CCD, its broad spectral sensitivity, could well render your results meaningless unless filters are used.
Filters, filter systems and which system should you use.
The simplest filter that you can have is a piece of coloured glass or plastic which allows only a limited range of wavelengths to pass. Limited in this context has to be defined. The Earth's atmosphere is already a filter allowing no significant amount of light to pass to the blue side of about 320 nanometres, (0× 32microns) and only intermittent bands of transmission to the red of 1,000 nanometres (1 micron). In addition we have shown above that even for this limited range of colours it does not transmit them all with equal efficiency. The human eye is also a filter. Thus we can detect from about 400 nanometres to about 700 nanometres, which means that we cannot even detect all the various colours that the atmosphere is capable of transmitting. Therefore, when we say that a filter should pass only a limited range of wavelengths or colours we mean limited compared with the response of the human eye.
Professional astronomers make use of several tens of different filter systems, some of which have been developed for very specific purposes such as the isolation of spectral lines of a single chemical element. There are essentially two types of filter which could be used. They are called interference filters and coloured glass filters. Interference filters are generally designed to provide narrow transmission bands (10 to 0× 1 nanometres). They are built up from several thin films, partially reflecting layers which act as a single or multiple Fabry Perot interferometer. The spacing between the layers is chosen to give constructive interference of the wavelength which the filter should pass and destructive interference for all other wavelengths. The optically active layers are typically vapour deposited and have their thickness controlled to a fraction of a wavelength of light. Side bands of light, which are not wanted, but which are transmitted by the interference part of the filter are blocked by additional layers of other multilayer blocking filters and colour glass filters. These multiple layers are optically cemented together to form the final filter. In the small quantities which are used by astronomers they are expensive to manufacture, typically a few hundred pounds each. However, that is not the worst of their problems. Firstly, they will only produce their nominal characteristics when used in parallel light at normal incidence, that is perpendicular, to the filter. If they are used in converging or diverging light, or the filter is tilted to the optical axis of the telescope, then their transmission will not be the same as the filter was designed for. Typically, the central peak of transmission will be shifted to shorter wavelengths, the transmission efficiency will be reduced and the width of the pass band will be increased. If the angle of incidence is 10° then the wavelength transmitted will shift about 1%. If the angle is 20° then the shift will be 2-3%. This would not be a disaster if the filter was designed to have a pass band width of, say, 50 nanometres but if it was designed to have a pass band width of one nanometre then the effect of a 1% wavelength shift could be enough to move the filter transmission completely outside its original specification.
If this were not enough the filters are also sensitive to temperature. If the filter expands then the distance between the optical layers increases and the filter transmission increases to longer wavelengths. Typically this shift is about 0× 003% per °C which might seem negligible. However, if you observe in an area where the difference between summer and winter night time temperatures is 30°C then you are back at the 1% level again for the shift. Finally, and most damming of all is the fact that this type of filter ages. Typically, water vapour enters the optically active layers through the edges of the filters. This process might take one or several years and can be delayed by coating the edges of the filter with modern epoxy resins. However, after some time the layers will be thicker than they were and once again the filter no longer has its original design characteristics. In short, these are not the filters which we would recommend for use by the average self financing observer.
The alternative type of filter is the coloured glass type. In these, coloured glasses are used which transmit light to one side of a given wavelength and absorb it at the other. The filter is typically composed of two, or more, pieces of optically flat, polished, coloured glass which are optically cemented together. One piece of glass is used to cut off the light to the blue of a certain colour while the other cuts off the light to the red of a similar, but slightly redder, colour. Where the two transmission bands overlap is the transmission of the composite filter. This type of filter has a long and honourable history of use and much of what we understand today about astronomy is due to the use of them. The pass bands, which they produce, are typically 60-100 nanometres wide and they are not adversely sensitive to converging light or light which is not passing through them at other than normal incidence. They are sensitive to temperature to the extent that their central wavelength can change by about 0× 1 nanometre for every 1°C temperature change. The large width of their transmission band prevents this from being a serious problem but whenever it is possible to design a system from scratch which allows the filters to be housed in a temperature controlled environment this can only aid the stability of the filter system.
This type of filter has much to recommend its use for self financing astronomers. It is cheap, typically tens of pounds each, and very importantly it does not suffer from ageing. In the present context this is a definite advantage for it means that once purchased there should never by any need to replace the filters. This long term stability is even more important scientifically for one of the very useful things which the home based astronomer can do is to monitor objects with variable brightness over long periods of time. You might choose to observe a system with a short period, which means that after obtaining one, or a few, nights data you can publish an analysis. However, as an alternative, one thing that you can do, which is becoming increasingly difficult for professional astronomers to obtain funding for, is to monitor objects that might vary over years, centuries or even millennia. We are already benefiting from the observations taken by careful amateur astronomers 100 years ago. By using a filter system with long term stability you can lay down a database secure in the knowledge that astronomers at unknown dates in the future can use your results to investigate problems that we might not even by able to imagine now.
The U B V R I system
The system of filters which we recommend that you use is that developed by Harold Johnson in the USA in the years 1940-1960 and Gerald Kron in the USA and Alan Cousins in South Africa in the 1960s and 1970s. It is based upon the use of five coloured glass filters, one for the ultra violet, U, the blue, B, the visual, V, the red, R and the near infra red, I. Figure 3 below shows the transmission bands of these five filters.
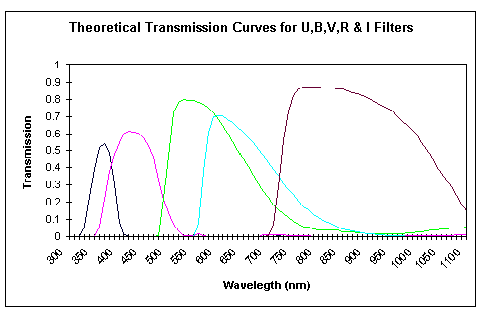
Note that the U filter stretches from nearly 300 to beyond 400 nanometres. This means that it is cut into by the ultra violet atmospheric cut off. If you look back to figure 2 you will see that it also brackets that area where the amount of extinction caused by the Earth's atmosphere is changing most rapidly. This means that it will be most readily affected by slight changes in the atmospheric extinction coefficient and that you will have more difficulty obtaining highly accurate results with this filter than with any of the others. Additionally, many CCDs are either insensitive, or have a rapid reduction in sensitivity, to the blue of 400 nanometres, so that it is possible that your system will not allow observations in this band. However, it contains information of great scientific value, and with all its faults, observations in this band can be very worthwhile. If your equipment will allow you to observe with this filter, and you are prepared to exercise the care and patience that observing near to the limits of the Earth's atmospheric transmission requires then this filter can be used by the home observer.
The other four filters have none of these problems. The B, V, R and I filters sit well away from atmospheric cut offs and are well within the sensitivity range of CCDs. The peak of sensitivity of most CCDs lies near to the V and R bands and if you could only afford to use one filter then there would be much to be said for making that the V filter. It approximates to the estimates that have been made by visual observers over centuries and coincides, as near as is possible, to the millions of V band observations taken over the last century. Thus your results can immediately be compared with those of thousands of other observers.
The exact specification of which types of glass should be used to make the filters is something which is often the subject of debate. It has to be realised that the original U, B, V system was created just after the development of photomultiplier tubes when the response of the photocathodes in these tubes to different colours was very different to that of CCDs. Early photocathodes were much more sensitive to blue light than they were to green light and they had virtually zero sensitivity to the red of the V band.
This meant, for example, that it did not matter that the glass which was specified for the U filter also passed light near to 750 nanometres as the photomultiplier tubes were totally insensitive there. A little thought will soon make it clear that the actual response of a photometric system is a result of what filters are used and the sensitivity gradient of the detector. Suppose that we use the same filter with two different detectors, one of which has a sensitivity which is increasing to the red across the filter and another which has a sensitivity increasing to the blue across the filter. What will happen is that the effective centre of the filter/detector combination will move to the red in the first case and to the blue in the second case, just as we described earlier in the section on atmospheric absorption in the context of hotter and cooler stars. This situation has existed with photomultiplier tubes for many years as the sensitivity of photocathodes has gradually been extended to the red when compared with the earlier systems. With CCDs the problem is only a matter of degree, not one of principle.
If all CCDs had exactly the same sensitivity versus colour curve the number of problems waiting to catch the unwary would be reduced. It would only be necessary to design one new set of filter combinations and, if we all used the same type of telescope optics, we could all use the one type of filter set as a standard. Life is not that simple of course. At the top end of the scientific scale there are CCDs which have phosphor coatings which emit visible light when ultra violet light falls on them. This allows them to be used in the far ultra violet. Other CCDs are thinned and illuminated from the rear to increase their ultra violet response. Even with the lower cost, mass-produced CCDs which tend to be used in the CCD cameras aimed at the home observatory there are quite serious changes in the sensitivity curve from model to model. Therefore, it is not useful to try to produce a set of filters which exactly mimics the original central wavelengths and widths of the early photomultiplier tube systems. Rather, it is better to resort to the strategy, which photometrists have been using for years, and to have filter sets which are approximately correct and then to calibrate your system on standard stars and to apply a correction to your observations to make them agree with the standard system. We will describe how to do this later.
In the figure below we demonstrate some of the variations which occur when one filter, the V filter in this case, is used with a variety of CCD chips. Note that the V filter lies close to the maximum sensitivity of most CCD chips and the effects would be much worse for the U and B filters.
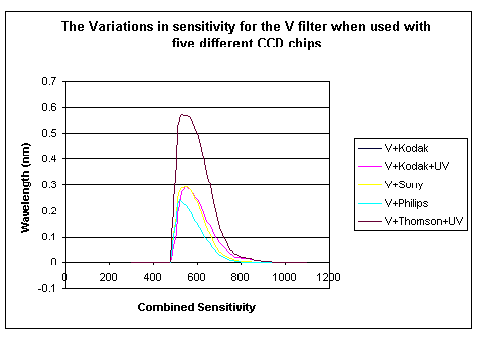
Note that the first two combinations, the V + Kodak and V + UV enhanced Kodak are superimposed as the UV enhancement does not affect the sensitivity of the CCD chip at this wavelength.
Although it might seem to be tedious and time consuming to have to do this, remember that it only ever had to be done once for your system unless you change something. Your alternative is to use a filter which gives as close an agreement as possible with the standard system and to rely on the fact that the field of view of the CCD is so small that you can obtain delta magnitudes which are 'approximately in the standard system'. If you do this it is important to state what your results are, i.e. approximately B or V etc. Before you decide to do that though, go back and look at the equations which were given in the earlier section on atmospheric extinction. Note, that in those equations, the (B-V) colour is multiplied by 0× 03, or a similar value, and the air mass (sec Z). Unless you use comparison stars which have identical colours to the variable you are trying to monitor, and many variables, not just supernovae, change their colours, then you will be introducing errors of several hundredths of a magnitude. This might not matter for some projects where the amplitude is large or only the timing of a maximum or minimum is required. However, for other projects which your CCD is well capable of, you could be introducing noise comparable to, or even larger, than the signal that you are trying to detect.
Below we give the specification of the coloured glass combinations which the author provides under the STARGAZER name. These will give you reasonable agreement with the standard U, B, V, R, I system.
|
Stargazer Photometric Filter Set |
|||
|
Filter |
Glass 1 |
Glass 2 |
Glass 3 |
|
U |
1 mm UG 1 |
2 mm BG 40 |
1 mm BG39 |
|
B |
2 mm GG 385 |
1 mm BG 12 |
1 mm BG 39 |
|
V |
2 mm GG 495 |
2 mm BG 39 |
- |
|
R |
2 mm OG 570 |
2 mm KG 3 |
- |
|
I |
4 mm RG 9 |
- |
- |
|
CLEAR |
4 mm WG280 |
- |
- |
Note that with the STARGAZER filter sets each of these filter combinations is further protected by the addition of quartz cover plates as experience has shown that some of the glasses used suffer from surface deterioration when exposed to the damp conditions experienced in many observatories. The ‘clear’ filter is provided as a replacement for those who do not use the U filter in order to remove the need to refocus the telescope between filtered and unfiltered positions.
In all of this it should be recalled that the central wavelength of the filters will move with temperature and that CCDs produced by different manufacturers have different response curves. Therefore, no matter how hard we try, we are not going to come up with a system which for the highest accuracy will not need to have corrections applied to bring it into line with the standard system
Positioning the filters.
Every optical surface which lies in front of your CCD chip can at some stage have dust land on it and stick to it. Every speck of dust which sits on each of these optical surfaces acts like a pinhole camera and casts an image, a shadow, of the entrance pupil of the telescope. It makes no difference whether the optical surface is a filter or a window to protect the CCD chip itself, the effect will be the same. The size of the shadow cast by each speck of dust will depend upon the f/ ratio of the telescope and the distance of the surface from the CCD. The faster the f/ ratio for a given distance the larger will be the shadow. The greater the distance for a given f/ ratio the larger will be the shadow. The larger and more opaque the speck of dust the more dense will be the shadow. You might think that you do not have this effect as your surfaces are spotlessly clean. Try this test. Take a flat field exposure, timing the exposure so that the majority of the pixels are as near as possible to being saturated without actually being saturated. Check this by inspecting the histogram of the pixel count against signal which comes as part of the control software for almost every CCD system. Now enhance the contrast to the maximum amount possible by selecting the most heavily exposed part of the histogram and expanding it so that it covers the full range of eight bits, or whatever your system is capable of displaying. Do you still believe that there is no dust in your system? It is possible that if you have just bought a new system, or just cleaned your old one, that your surfaces are truly clean. They are unlikely to stay that way. Below we show an image taken from the monitor showing this effect on a 10" f/10 Schmidt-Cassegrain telescope.
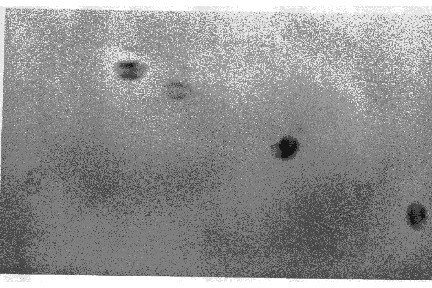
If you want to carry out accurate photometry then it is vitally important that the shadows cast by dust and which will affect your flat field calibration are always in the same position. If they are not then your flat fields are not being applied properly. Currently pixel sizes on CCDs tend to lie in the range 6.8 to 25 microns. If you are to obtain the best photometry that your system is potentially capable of then it is important that the optical surfaces which can carry the dust are fixed to a small fraction of a pixel size. If you only have one filter and it is never removed then that is not a problem. However, if you have a filter wheel containing, say, five filters plus a previewer system then care has to be taken to ensure indexing of the filters to about a micron. Mechanically this is a non-trivial task.
Below we show a photograph of the Stargazer filter and previewer system, designed and developed in England, to give amateur astronomers access to a professional quality system. In this case the indexing of the six position filter wheel is done by a wide, flat area on the circumference of that wheel for every position and it is impossible to measure any departures from perfect indexing. Thus any errors are well within the size range required by small pixels. Note also that a prism giving a 20 mm unvignetted field of view is also included to aid rapid acquisition of the correct field when small area CCDs are used

Photon Statistics, full well capacities, A/D converters and the ultimate accuracy of your results.
If you had perfect instrumentation, a perfect sky, a telescope which tracked perfectly and the best CCD in the world you might be forgiven for believing that there would be no limit to the accuracy with which you could do photometry. In order to understand why this is not the case one has to consider the nature of light and some of the limitations which this imposes. Additionally the fact that your CCD electronics are not perfect creates further constraints upon the ultimate accuracy which can be obtained. No matter how hard you try, there will always be some error associated with your measurements. To explain why, we will deal with the limitations one at a time.
It is fundamental to the nature of things that it is not possible to measure anything with perfect accuracy. This applies just as much to measuring the length of a stick as it does to recording the number of photons which have been captured in one pixel of your CCD. The nature of light is such that there are additional problems with measuring how much light comes from a given object in a certain amount of time. The scientific term which is applied to measurement of these errors in the case of light is 'Poissonian Statistics', named after the scientist, Poisson, who first determined them. The essence is that the ultimate accuracy with which you can determine the quantity of an amount of light varies as the inverse square root of the number of photons you have recorded. Suppose that you have recorded one million, 106, photons, the square root of 106 is 103 and so the ultimate accuracy of that measurement is 1/103 or one part in one thousand which is 0× 001 magnitude. The table below shows the ratio for several values.
|
Total Counts |
Maximum Possible Accuracy (fraction) |
MaximumPossible Accuracy (magnitude) |
|
100 = 102 |
0× 1 = 10-1 |
0× 11 |
|
10,000 = 104 |
0× 01 = 10-2 |
0× 01 |
|
1,000,000 = 106 |
0× 001 = 10-3 |
0× 001 |
You should note that this limit on accuracy also applies to low counts such as are obtained when you are taking dark frames. Suppose that you have a low noise CCD chip, well cooled and that it only records one dark count every five seconds. If your exposure time is 100 seconds then you are only going to have about 20 counts recorded. The error on only 20 counts is ±22%, which means that the recording of many dark frames and taking their mean or median is required if an accurate figure is to be obtained. We will return to this matter later but before we do we have to consider the ability of your CCD to record and read out counts. The total amount of signal, which can be recorded in each pixel of your CCD, is known as the 'full well capacity'. If you have a CCD with 9 micron pixels then it is likely that the full well capacity of each pixel will be about 70,000. If you have a scientific quality CCD with 25 micron size pixels then the full well capacity could be about 400,000. The best possible accuracy from the first is about 0× 004 magnitudes and from the latter about 0× 002 magnitudes, both of which put you well within the range of being able to do useful work.
You should never exceed the full well capacity of your CCD's pixels. This is the equivalent in photographic terms of saturating an exposure. You will not actually harm the CCD but the counts will be meaningless. Some CCDs have what are called 'anti blooming drains' to bleed away this excess charge and you should find out whether your own system has this feature. If it has, then you need to experiment very carefully with exposure times as you can be fooled into believing that you have not overexposed when in fact you have and the excess charge has been removed. Parenthetically, if you have not yet bought a CCD camera then we would urge you not to buy one with anti-blooming drains. There are several reasons for this. Charge is being bled away the whole time which means that the sensitivity is reduced. The rate of charge removal is a function of how large the pixel charge is; the larger the charge, the greater the leakage. This means that the detector is no longer linear, thus loosing one of the great advantages of the basic CCD chip. Careful experiments on CCD chips which have anti-blooming drains, but with the electronics modified to cut down as much as possible the anti-blooming leakage, suggests that under the best circumstances and with exposures being limited so that no pixels are more than half full, linearity over a range of better than three magnitudes is possible. It is this author’s view that it is better to start with a CCD chip without anti-blooming drains.
In addition to the above your CCD has an analogue to digital converter (A/D) which converts the charge in each pixel into a number. Typically these A/Ds are 8 bit, 12 bit or 16 bit. The decimal equivalents of these binary numbers are 256, 4096 and 65,536. You will now see that there is an additional problem in that even with a 16 bit A/D you might wish to try to read out a number as high as 400,000 with a device which can only really count up to 65,536. One solution would be to use a higher bit A/D but great care has to be exercised. It is vital that your A/D should be linear over its whole range. Higher bit A/Ds do exist, such as 18 bits, but when tested for linearity they are found to be less linear over 16 bits than good 16 bit devices. Therefore, the solution which is normally adopted is to scale the counts by a constant, say 8 in this case, allowing the full well capacity to be read out. Of course this now causes problems at the other end of the scale. It means that when trying to record low counts, such as when taking dark frames you can no longer record 0, 1, 2, etc but only 0, 8, 16 and so on.
Suppose that you have gone to the trouble and expense of buying a very low noise CCD and cooling it well so that with exposures of only a few tens of seconds you have dark counts of about 10, with a further 10 due to read out noise, that is a total count of about 20 per pixel. Due to the scaling, a factor of eight in the example being used, this will be read as either a 16 or 24, that is an uncertainty of up to about eight. This number has to be subtracted from the counts of the star which you wish to measure. Clearly, if you are working on a star near to the saturation of the best of the CCD chips with a count of about 400,000 per pixel (potential accuracy 1 part in Ö 400,000 = 1/632) then an uncertainty of 8 is going to have a negligible effect upon the accuracy. Even if you have a small pixel chip with a full well capacity of 70,000 (1 part inÖ 70,000 = 1/265) then there is still not a serious problem. However, suppose that on the same exposure you have stars which are five and ten magnitude fainter than the saturation level of the CCD chip. These will have counts of 4,000 (potential accuracy 1 part in Ö 4,000 = 1/63) and 40 (potential accuracy 1 part inÖ 40 = 1/6) for the larger pixel CCD. For the smaller pixel CCDs, with the lower full well capacity, the equivalent numbers will be 700 (potential accuracy 1 part inÖ 700 = 1/26) and 7 (potential accuracy 1 part in Ö 7 ~1/3). You are now starting to learn about some of the restrictions of using CCDs for photometry. Note that these figures are assuming that there are no extra sources of error. In reality of course there always will be. Therefore, notwithstanding the fact that you might be able to see stars which have a magnitude difference of between five and ten on your monitor there is a real limit to the accuracy with which these can be measured. The combination of full well capacity in the current generation of silicon based CCDs and the limitations of 16 bit A/Ds conspire with the laws of photon statistics to produce constraints of which you have to be aware. Note that if you have a system with only an 8 bit or 12 bit A/D then the situation is even worse. Some of the variable stars which you might well wish to monitor could have brightness variations of over five magnitudes, eruptive variable and eclipsing binaries for example. None of this should be taken to imply that you cannot use your CCD to work on star fields or variables with a wide range of magnitudes. However, you must be aware of the limitation of the system and plan your observing strategy accordingly.
There are two other dangers which are generally ignored but which you need to be aware of when you wish to obtain the maximum accuracy from your CCD for photometry. The first of these applies only to those who wish to make short duration exposures and is due to the nature of any mechanical shutter which is used to control the exposure time. Typically these consist of an opaque, low mass arm which is normally in front of the CCD chip. At the start of the exposure it is moved to one side and at the end of the exposure it then returns from that side to stop the light falling on the CCD while it is read out. This shutter arm cannot be moved infinitely quickly and typically it will take 0× 01 to 0× 02 of a second to move its full distance. Therefore, one side of the field will have an exposure perhaps 0× 04 of a second longer than the other. It might be thought that this would be taken out with the flat field exposures but a little thought will show that this is not the case. Your flat field exposures are likely to take several tens of seconds and for these the differential exposure of one fiftieth or one twenty-fifth of a second is negligible. Suppose now that you use your CCD to make very short exposures either of a bright star, a planet, the solar surface etc. If this exposure has a one second, or less, duration then the shutter differential can start and be a significant fraction of the total exposure.
The only way round this is to ensure, that for these specific types of exposure, that the duration of the flat field exposure is as short as the exposure you wish to take for scientific purposes. There are three alternatives. You could use a system which has a double shutter where the shutter which ends the exposure moves across the chip from the same side as the shutter which starts the exposure. Alternatively some systems use electronic 'shuttering' either by transferring the stored signal into columns of pixels adjacent to the columns storing the real image and which are there purely to act as a frame store. These are called interline transfer chips. The final alternative is to use a system where part of the CCD chip itself is used as the store. In these, half the area of the CCD is blanked off and the image from the optically active half is rapidly transferred to this blanked off area prior to being read out via the A/D converter. These are called frame storage chips.
The other potential source of error, which is often overlooked in CCD photometry, is the cloudiness of the sky. Traditional, single channel, photoelectric photometry is just about impossible unless sky conditions are good. Transparency variations due to passing clouds, even clouds so faint that they cannot be seen with the naked eye, can often be tens of percent. There can be the erroneous assumption made by CCD users new to the field of photometry that transparency variations due to clouds will average out over the field of view because the fields of view are small and the images are all obtained simultaneously. If the exposure is several minutes duration and the clouds are moving rapidly then this assumption might be valid. However, if the clouds are slow moving, sharp edged cumulus, alto cumulus or similar, and if the exposure time is short then the assumption might not be valid. If you are using a large area CCD with a short focal length system so that the field of view is large then even more care has to be taken with this potential source of error. If the project which you are engaged in requires high accuracy photometry and if there is any doubt in your mind about the quality of the sky then take several exposures. Measure the magnitudes on each one and then calculate the mean and standard error from all the measures. The standard error thus obtained gives you a scientifically valid measure of the accuracy of your results. This can be used to prove to others, who might question your measurements, just how accurate your results are. It gives a measure, not an opinion, of the validity of your observations and that is part of what science is about.
Two ways in which you can obtain photometry of point sources from your images.
It is highly likely that if you bought a CCDs system, as opposed to building your own, that it came with a software package which included a method of doing photometry. There are two different ways in which this is carried out and the user needs to know which method is being used and what its limitations are. The most generally available method, and the one which is least demanding mathematically is the analogue of aperture photometry. In this method you are asked to specify an area of the image, typically 3 x 3 pixels, 5 x 5 pixels, 10 x 10 pixels and so on. This is represented on the screen by a square which you can drag with your computer's mouse, or other pointing device, and which you centre on the stellar image of interest. The software quite simply adds up the counts in all the pixels in that area and derives a total.
Of course some of the signal in the box will be due to the sky and dark counts only and therefore you also have to position the box on a part of the image where there seems to be no evidence for a stellar image. The total count in this area is then stored as a constant which has to be removed from each of the boxes which contain a stellar image. Thus your original box which contained a total signal due to (star+sky+dark) has (sky+dark) removed to leave (star) only. This is done for each stellar image in which you are interested, possibly the variable plus six to ten comparison stars, and thus you have a measure of the intensity of light which was coming from each of the stars during the exposure. These intensity measures now have to be turnd into magnitudes, to put them onto the established traditional system as described earlier and the differences taken so that you end up with a series of D magnitudes between the variable and the comparison stars. To convert from intensity to magnitude the equation is
magnitude = -2× 5 log10 (intensity)
There are two things to note about this equation. The first is the negative sign in front of the 2× 5 which means that as the brightness gets less the magnitude gets more positive, i.e. larger, in keeping with the standard system in which a star of magnitude six is fainter than a star of magnitude one. The other thing to note is the numerical value of 2× 5. This is not to be confused with the value of 2× 512, the fifth root of 100, which we referred to above when describing the origins of the magnitude scale. Variations on this basic method include using a rectangle or circle as the defining aperture. This method will work perfectly provided that the field of view which contains the stars of interest is not too crowded. If you can see apparently clear sky around each image of interest, and this is large enough to contain your defining aperture, 5 x 5, 10 x 10 etc., then there is no need to choose any other method. A word of advice is in order here. Traditional photoelectric photometrists have found that the best accuracy is obtained when apertures of about one arc minute are used. If your observed field is not too crowded then use a generous array of pixels for your measurements.
The problem arises when you wish to derive magnitudes for stars in a crowded field of view, possibly a cluster or in the plane of the Milky Way. Here the proximity, possibly even overlapping, of the images precludes the use of even small, discrete apertures and one has to resort to modelling the profiles of the stellar images. The models used to represent the stellar image can range from the Gaussian profile, a well established curve which applies to the distribution of many things such as the height of human beings, IQ measures and so on, a Poissonian profile, similar to, but subtly different from, the Gaussian and the 'point spread function', PSF, which is the empirically determined profile of the real stellar images as derived from several of the brighter and best separated images on the exposure. The idea is that the spread of the image on the CCD, and the number and distribution of counts with the image should conform to a standard pattern which will be the same for stars of all magnitudes. The only difference will be the scale of that standard profile; large for bright stars and small for faint stars. Figure 6 below shows the idea in graphical form.
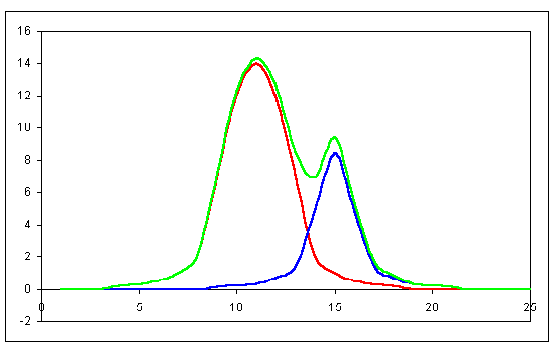
Several software packages supplied for CCD image analysis now include this method as an option. There is nothing to stop you using it with well separated star images but it is not necessary and the aperture method will work fine in those cases.
Finally there is one other area of photometric reduction which is sufficiently specialised that it will only be of interest to a few readers. However, the general reader should be at least aware of its existence. If you wish to work on really crowded fields of several hundred stars, perhaps to obtain a colour/magnitude diagram of a whole cluster, then there are several powerful weapons in the armoury of computer based analysis. They rely on iteratively re-analysing the data to search for global minima in the distribution of the residuals and errors. They all rely on fitting a profile, such as the 'point spread function' mentioned above. One method is called 'simulated annealing' and is a mathematical analogue of what happens when a piece of metal is annealed. During this process the metal is heated so that the individual molecules have enough energy to be relatively mobile and then the metal is cooled slowly enough so that the molecules are allowed to migrate to low energy levels in the crystalline structure of the metal. The trick is that the slowness of the cooling allows occasional movements to higher energy levels so that what happens is that eventually the whole system finds a global minimum rather than just a local one. This reduces the brittleness of the metal and allows it to survive many more stress reversals than would otherwise by the case. The mathematical analogue takes all the profiles of the individual and overlapping stellar images and iteratively re-computes their energy distributions to give a global minimum. All the methods for crowded field photometry seek to minimise the residuals but the trick with the 'simulated annealing' method is that the reduction in the residuals is subject to a random walk algorithm which allows occasional departures to higher energy levels. The idea is that by allowing the solution to wander about it will avoid settling in a local minimum and find the true global minimum for the whole data set. These methods are computationally intensive and take large amounts of computer time. You will typically have to leave your computer to get on with the reductions for several hours. This might increase to a significant fraction of a day in the case of the 'simulated annealing' analogue even with a powerful personal computer. Several of the software packages to carry out this work are available commercially or can even be downloaded free of charge for those with access to a modem and email or the Internet.
Reducing your observations to a standard system.
We have explained earlier how changes in the transmission of the Earth's atmosphere and different colour responses of different types of CCD mean that for the best accuracy you should apply some corrections to the basic D magnitudes which you will obtain from your CCD images. Remember, the problem is that the widths of the U, B, V, R, and I filters are large enough that the gradient of the atmospheric extinction and the sensitivity curve of the CCD can effectively alter the centre of response for each filter so that it is to the red or blue of its nominal position. The corrections we will describe below are designed to determine the size and effect of these changes and to compensate for them.
In order to understand why the corrections have the form that they have it is first necessary to understand the nature of conventional, all sky, photoelectric photometry. In this it is normal to observe stars over a wide range of zenith angles and the stars of interest might be many tens of degrees from the stars being used as a reference frame. Because the stars are likely to have very different colours as well as very different zenith distances it has traditionally been necessary to devote a great deal of effort to the determination of a set of standard stars and to determining the corrections and constants which allow other observers to put their observations onto the standard system. The corrections include the values to allow for filter central wavelength shifts due to sky, detector and stellar temperature. The constants are required to reduce observations from large and small telescopes, refractors and reflectors etc to one common scale. The best observers in the best sites can produce magnitude measurements by these means with standard errors of about 1%, (0× 01 mag.).
Of course most of the world's observers do not live in good sites and are what might be termed 'photometrically challenged'. It is seldom that all sky photometry accuracies of 0× 01 mag. are obtainable for most people and therefore for the most accurate work, with errors typically near to 0× 001 mag., it has become normal to do what is called differential photometry. In this method the variable of interest and the comparison stars are chosen to lie within a few degrees, or less, of each other on the sky and no attempt is made to apply zero point corrections or scaling factors. Instead. a list of D mags. is obtained. Of course, if these are to be really accurate to 0× 001 mag. then corrections to allow for the colour of the stars etc. must still be applied. Exceptions apply only in those rare cases where the variable and comparison stars are known to have the same colours and spectral types or where the stars can be observed at the same zenith distance on every night.
The type of CCD photometry with which we will deal below is the direct equivalent of differential photometry. The small size of CCD chips might cause frustrations as it sometimes means that the comparison stars, which have been used for years for some variables, are outside the field of view and new comparison stars have to be used. However, in the context of differential photometry the small sizes ensure that a small field of view is obtained on most telescopes, which in turn means that the range of zenith distances across the field is also small. Thus, for a single exposure there should never be any need to apply differential corrections across the field. Corrections, which depend upon the colour of the star, must, of course, still be applied if high accuracy is required. Note that occasionally CCDs are used for all sky photometry when they are used to replace photomultiplier tube, (PMT) systems. In general this is not a good idea as the full well capacity limitations and non photon counting operation of CCDs restricts their potential accuracy when compared with PMTs. If they are used in this mode then it is important to apply the full range of corrections.
The standard equation which is used to correct observations for both atmospheric extinction and the colour of the star is:-
M = Mobs + M0 + k' .X + k'' .X (B-V) (1)
where M is the true magnitude, Mobs is the observed magnitude, M0 is the instrumental offset, X is the air mass, (B-V) is the colour index of the star, k' is the extinction coefficient for a specific filter (that is, how is the quality of that night's sky affecting a particular filter, irrespective of the colour of the star) and k'' is the colour dependent coefficient which depends upon the colour sensitivity of the filters, the CCD and the optical system. M0, k' and k'' will be functions of which filter is being used.
It is worth looking at this equation in some detail in the context of differential photometry across the small area of a typical CCD. Provided that you have one star in the field, which has well-known magnitude and colours, then you can use that star to give you your M0 and all your magnitudes can be referred to that if you wish to produce a list of magnitudes, rather than D magnitudes. The part of the equation which reads k'X can also be ignored, as the small field of view of your CCD will mean that the whole field effectively has the same X. That only leaves the colour dependent part of the equation; that part containing k''. This part cannot be ignored if you wish to work to the ultimate accuracy of your CCD. The only way that you could get round the need to apply this correction is if your variable and all the comparison stars have the same, or very similar, B-V colours and spectral types. Note that qualification. It is possible to find two stars with the same B-V but grossly different spectral types because the hotter (bluer) star is reddened by interstellar absorption. Although these stars might have the same B-V they would be different in other colours, U-B or R-I for example. Note that if the variable which you wish to observe, significantly changes its colour with time then it would be meaningless to try to use an uncorrected system of reference star magnitudes. The other exception is if you live in a climate where it is possible to observe at the same zenith distance night after night. Most of us are more photometrically challenged than that.
In order to determine the value of the k'' term you have to observe stars of known, but different colours, over a wide range of zenith distance (air masses). You can either observe a small group of stars or, in the simplest case, a red/blue close pair of stars. It is important that the magnitudes and colours of the stars are well determined and the stars should be chosen to have as wide a range as possible in (B-V). The actual practise of determining these corrections is about as simple a job as it is possible to do. One observes the pair, or group, of stars over as wide a range of air masses as you can, from the meridian down to as near to the horizon as you feel it is practical to go. You should observe using all the filters for which you wish to calibrate the system. A typical observing session could be on a pair of stars starting near to the zenith and using all of the U, B, V, R and I filters. You would then repeat this sequence. As the Earth rotates and the stars move to larger zenith distances you will start and build up a set of exposures which allow you to measure how the brightness of the blue star changes relative to the brightness of the red star. As mentioned earlier the absorption due to the Earth's atmosphere is less in the red than in the blue and hence the red star will appear to brighten relative to the blue star as they sink down the sky.
A word of warning is in place here. Above we have included the U filter in the sequence. Many CCDs are insensitive to U band wavelengths and if you have one of those then you can ignore that filter. Even if you can observe in the U then you should understand that we have included that filter so that you can compare its results with regard to scatter etc. with the other filters rather than derive and use an independent k'' extinction coefficient for that colour. The reason for this is as follows. When Harold Johnson set up the UBV system in the 1940s and 50s he made the explicit assumption that the extinction coefficient in the U would be the same as that in the B. Later experience has shown that this is not the case but unfortunately by the time this was realised the UBV system was already well established and the system was actually defined to have the same extinction coefficients for these two colours. If you do not have the possibility to use the U band then it will require very little extra effort to include it in your observing sequence and to determine what extinction coefficient you really get. The scatter, when compared with that in the other bands, will also be informative as to what accuracy you can work to in this colour. You can use your new determination of k'' for the U band and get better accuracy, but if you do you cannot claim that your results are on the standard system. Before you can carry out this observation and reduction you will need to know two things; how to calculate the zenith distance or air mass and fields, or pairs, of stars with a wide range of colours. Below we give two equations to allow you to calculate the air mass and a table of close pairs of stars with red/blue components.
The secant of the zenith distance can be calculated from the equation:-
sec z = 1/( sin f ![]() sin d
sin d ![]() + cos f
+ cos f ![]() cos d
cos d ![]() cosh) (2)
cosh) (2)
where z is the zenith distance, f ![]() is the observers latitude, d
is the observers latitude, d ![]() is the stars declination and h is the stars hour angle. This equation is approximate and relates to a flat Earth model with a plane parallel atmosphere. An equation to calculate air mass, which should give more accurate results at large zenith distances and which accounts for the fact that the Earth is spherical and the atmosphere progressively decreases in density with altitude, rather than just coming to an end is:-
is the stars declination and h is the stars hour angle. This equation is approximate and relates to a flat Earth model with a plane parallel atmosphere. An equation to calculate air mass, which should give more accurate results at large zenith distances and which accounts for the fact that the Earth is spherical and the atmosphere progressively decreases in density with altitude, rather than just coming to an end is:-
X = sec (z) - 0·0018167 [sec(z) - 1] - 0·002875 [sec(z) - 1]2 - 0·0008083 [sec(z) - 1]3 (3)
where X is the air mass and z is the zenith angle. Note however, that the constants in this equation relate to a good, high altitude site. They will be different for poor sites.
An alternative, simpler equation, due to Andrew T. Young, which can be used to derive X, the air mass, and which should work down to a zenith distance of 78°
(sec z = 4), is :-
X = sec z [1 - 0·0012 (sec z - 1)] (4)
The table below gives details of several close red/blue pairs which can be used to determine your extinction coefficients. .
-21-
|
Pair |
HR |
SAO |
HD |
Sp. Type |
RA (2000) |
Dec (2000) |
B |
V |
B - V |
D (deg) |
||||
|
1A 2A |
1051 1052 |
38893 38890 |
21551 21552 |
B8V K3III |
03 30 37 03 30 34 |
+48 06 13 +47 59 43 |
5.78 5.71 |
5.82 4.36 |
-0.04 +1.35 |
0.11 |
||||
|
1B 2B |
1226 1229 |
56849 56866 |
24843 24982 |
gK1 A1Vp |
03 58 29 03 59 40 |
+38 50 25 +38 49 14 |
7.38 6.48 |
6.30 6.38 |
+1.08 +0·10 |
0.23 |
||||
|
1C 2C |
1534 |
112096 112098 |
30544 30545 |
B9 K1III |
04 48 39 04 48 45 |
+03 38 56 +03 35 18 |
7.26 7.22 |
7.32 6.02 |
-0·06 +1.20 |
0.06 |
||||
|
1D 2D |
4075 4081 |
62010 62019 |
89904 90040 |
A6V K1III |
10 23 06 10 24 08 |
+33 54 29 +33 43 06 |
6.03 6.68 |
5.88 5.50 |
+0.15 +1.18 |
0·29 |
||||
|
1E 2E |
6418 6436 |
65890 65921 |
156283 156792 |
K3II A2V |
17 15 03 17 17 40 |
+36 48 33 +37 17 29 |
4.60 4.70 |
3.16 4.65 |
+1.44 +0.05 |
0.71 |
||||
|
1F 2F |
|
122687 122686 |
161261 161242 |
B9 K2 |
17 44 15 17 44 11 |
+05 42 48 +05 14 58 |
8.36 9.08 |
8.31 7.80 |
+0.05 +1.28 |
0.46 |
||||
|
1G 2G |
|
145914 145916 |
210419 210434 |
A1V K3III |
22 10 21 22 10 34 |
-03 53 39 -04 16 01 |
6.26 6.98 |
6.27 6.00 |
-0.01 +0.98 |
0.38 |
||||
If non of the pairs of stars in the above table are suitable for your particular system because they are too bright or for some other reason then groups of stars in the magnitude range V ~ 9-13 have been measured by Landolt and the details are published in the 1973 Astronomical Journal, vol. 78, page 959 and the 1983 Astronomical Journal, vol. 88, page 439. Even fainter groups of stars are available in Christian et al. 1985, Publication of the Astronomical Society of the Pacific, Vol. 97, page 363 and again by Landolt in the 1992 Astronomical Journal, vol. 104, page 340.
The exact procedure which you adopt to determine the corrections is going to depend upon what software you have and where you live. We will explain both procedures in detail and hopefully convince you that it is a sufficiently easy task that you will not only do it but you might actually enjoy doing it. Understanding the more complex of the two procedures, even if you cannot use it yourself, will help you to understand the alternative method. The more complex of the two possibilities needs you to have two particular assets. The first is a software package which will produce magnitudes, not just D magnitudes, from your exposures and the second is a sky which at least on some occasions is truly photometric. You will know if you have a suitable software package as part of the procedure will have asked you for the size of the telescope, the f/ratio and other details so that the software can relate an image of a given density to a star of a given magnitude. What this software package does is allow you to use your system for all sky photometry. From a knowledge of the telescope's parameters, the time, the position of the observatory and the position of the stars the software will do its best to come up with sensible magnitudes for the stellar images. If, like most of the world, you are photometrically challenged then variations in the sky transparency will render this method meaningless.
Suppose that you have the correct software and a good sky. You will choose one of the red/blue pairs of stars above, or possibly one of the Landolt's red/blue groups. You will start and observe when the stars are on, or near to, the meridian and you will continue to observe until the stars are only about 10° above the horizon. The greater range of zenith distance and the broader the range of (B-V)s, the more accurate will be your final result. You will cycle through as many of the U, B, V, R and I filters as you wish to use in the future for your regular observing. When all the data is in and the magnitudes measured then you are going to plot some graphs. If you have access to a spreadsheet then both the plotting and some of the ensuing calculations will be eased. You will need to plot a graph of observed magnitude against air mass for each of the filters you used and the air mass, typically along the horizontal axis will start at zero. There is a reason for this although sec Z can never achieve the numerical value zero. Remember secant is 1/cosine and it equals one at the zenith and increases, in whatever direction you move from the zenith. However, it is normal to correct stars for atmospheric extinction, from whatever value of sec Z they were observed at, to the value that they would have had at sec Z = 0. That is, published catalogue values are corrected to above atmosphere values. You will plot a separate line of results for each of the stars of varying B-V colour which you have observed. Below we show two diagrams in order to illustrate what your figures should look like.
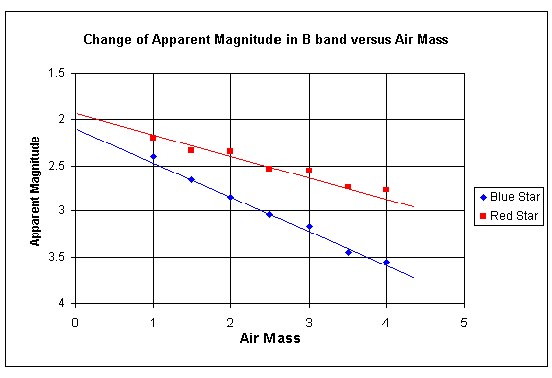 Figure 7
Figure 7
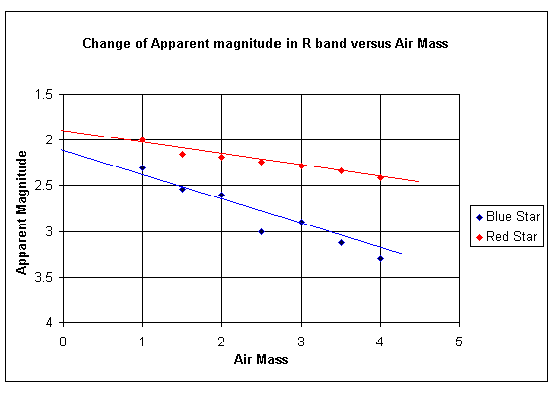 Figure 8
Figure 8
Note that each of the lines is straight apart from observational scatter. This would not be the case if intensities had been plotted on the vertical axis rather than magnitudes and it is one of the reasons that the use of magnitudes has persisted; not just to conform to an historical system. Also note that the magnitude value where each of the stars crosses the vertical axis at air mass zero is the catalogue value.
It should now becoming clear why this particular observing routine has been used. You will see that the gradient of how each star reduces in brightness (increases in magnitude) as the air mass increases is simply the value of the extinction coefficient, k', for each filter and for a range of (B-V)s. Notice how the change in magnitude for the red stars is less than that for the blue stars. Remember how at the start of this section we explained why the setting sun was red! If you compare the gradients on the B diagram with those on the R diagram you will see that the R gradients are lower, also showing that red light is less affected than blue light. The derivation of the k'' term is now trivial. You know the gradient for a blue star and you know the gradient for a red star. You also know the difference in the B – Vs of the two stars. You can therefore calculate the value of the k'' coefficient. Formally we can write it down as an equation:-
k'1 - k'2
k'' = _____________________
[(B - V )1 - ( B - V )2]
where k'1 and k'2 are the measured gradients of the two stars and (B-V)1 and (B-V)2 are the (B-V) colours of the two stars. Simply divide the difference in the k's by the difference in (B-V)s and you have your k''. Do this for each of your filters. You could, of course do this for any other colour index, (V-R) or (R-I) and indeed some professional observatories not only do this but also apply a correction for the (B-V) and the (R-I) in each reduction of an observation. The reason that we have not recommended that you do this is that the red corrections are generally very close to zero and it is likely that most of the readers of this book will restrict themselves to differential photometry across the relatively small field of the CCDs. However, if you wish to use your CCD to do serious all sky photometry then you should be aware that it is possible to develop a very thorough reduction technique to enable high accuracies to be obtained wherever the sky conditions allow,
What do you do if you do not have the all sky photometry software needed for the first method or if you live where you might have to wait for months before you get a night which will be photometric for six hours or more? If you have understood the above method then you should be able to guess the alternative, as it is merely a cut down version of method one. You cannot produce straight-line extinction gradients over a range of seven in air mass if the transparency of the air is constantly changing. What you can do is to do differential photometry over the same range in air mass. If you choose one of the red/blue pairs of stars in the table above and monitor their relative brightness over a wide range of air masses as they move from the meridian to the horizon then you will have the data that you need to determine k''. The change in relative magnitude over a wide range of air masses gives you the gradient for each filter and the difference in (B-V) is known. If you want to check your results then you can repeat the observations for another pair, or even several other pairs, of the red/blue stars and you can take the mean of the various determinations. The really good news is that once they have been determined they should stay constant for years, or until you change something. Check them every few months until you are confident of their stability and once a year thereafter, ensuring that any developing problems are detected before too much data is wasted.
It is likely that the numerical value that you get for k'' will be less that 0× 05 for B, and less than that for redder colours. What this means in practice is that if you do not determine and apply the corrections, if you use reference stars which have (B-V)s different from each other by one magnitude and if you observe your stars at a range of air masses from one to three then you could introduce avoidable scatter into the observations of nearly 0× 1 mag.
Choosing a system, practising and checking your potential accuracy.
The acquisition of new scientific knowledge does not come easily. If it did then it would have taken less time for us to move from the trees to the caves and on to where we find ourselves today. We are like people walking through a forest in that we cannot see the end of our journey nor can we even know what we will find round each new twist and turn. It might by a blind alley or it might be a whole new way forwards. In general, you will not know before you start a series of observations what you will find, but if your observations are of good quality and you keep a careful record of what you have done then the opportunity is there for you to make a real contribution to our understanding of the universe. Do not allow your prejudices or preconceptions to influence you. Do not throw away observations which do not fit where you think that they should, unless you know that they are faulty due to cloud or instrumental problems. You might be throwing away the one piece of new information that is needed to revolutionise our understanding of something. Finally, never even consider falsifying data. The brief fame which you might acquire will in no way compensate for the enduring contempt which your colleagues will hold for you when the truth emerges. In astronomy we seek to understand nature in the large; that huge, impersonal, backdrop of reality against which we can judge our hopes and aspirations. Our longevity as a culture, or even species, might one day depend upon our understanding of how, where and when we fit into the larger scheme of things.
In order for you to successfully produce scientifically useful results several things are necessary. Your telescope must be well mounted, your CCD must be matched to the telescope, you must learn to use your equipment in a competent manner and you must fully understand the potential accuracy of your system so that you only undertake projects where the variations are detectable by your equipment. We will deal with these items one at a time.
The telescope
If you already own a telescope you might be wondering whether it is suitable for CCD photometry. The answer is almost certainly yes, whether it is a refractor or a reflector, has a large diameter or small. If it is a refractor then it is unlikely that you can use the U band, but as many CCDs are insensitive there, that is hardly a problem. If it has an effective focal length which is not well matched to the pixel size of your CCD (we will return to this point below) then a Barlow lens or focal reducing lens can alter the effective focal length. CCDs are so sensitive that even small telescopes can produce real science and the aperture is more of a limit as to what brightness stars you can work on, rather than whether you can do science or not. Of much greater importance than either the aperture or the telescope type is the alignment of the polar axis and the accuracy of the R.A. drive.
It has become common for the manufacturers of mass produced telescopes to sell them with alt-azimuth mounts and some computer software that allows co-ordinate transformation to Right Ascension and Declination after the system is calibrated on a few bright stars at the start of the night. This might be fine for those who only wish to look through their telescope. However, it completely misses the point that astrophotography, with either photographic emulsion or CCD, on any telescope without a correctly aligned polar axis will suffer from field rotation. The wider the field the worse the effect. The longer the exposure the worse the effect. The worse the alignment of the polar axis the worse the effect. An image rotator can cure this effect but only at the cost of extra expense, complexity and light loss. It is not impossible to take scientifically useful images with a mobile telescope but if you wish to make life easy for yourself opt for a permanently mounted telescope and line up the polar axis carefully.
If you do not know how to line up your polar axis then the following is a foolproof method. You will need an illuminated graticule, a relatively high power eyepiece, a fine and repeatable method of moving the telescope mount in altitude and azimuth and patience. Find a bright star near to the meridian and the celestial equator and centre its image on the illuminated graticule. Allow the telescope to track the star for a few minutes and then note whether the star has moved north or south relative to the centre of the graticule. Ignore all east/west movement as this could be due to a faulty tracking rate and this method is designed to be specifically insensitive to such errors. Now make an azimuth (east/west) adjustment to the telescope mount and re-centre the image on the graticule. We strongly recommend that you keep written notes as you go along. You will be doing this in the night, you might be tired and it is going to take hours. Wait a few minutes and now check to see whether the image movement is better or worse than it was before. If it is better then you moved in the correct direction. If it is worse then undo the previous adjustment and repeat it in the opposite direction. After some time you will get a feel for how much adjustment is required and will see how the amount of adjustment has to be reduced as one gets nearer and nearer to the position where no movement is detectable.
When you are satisfied that you have this first phase of polar axis alignment fairly correct you should then move the telescope so that it is pointing approximately six hour east or west of the meridian. Again you should find a bright star near to the celestial equator and line it up on the graticule. Once again you are looking for north/south movement and ignoring any east/west movement. You repeat the whole operation as before except that this time you tune the altitude (up/down) adjustment of the polar axis. Continue until you do not see significant movement over a five minute period. Do not worry if this takes so long that the star you started with has set. Choose another one. The exact position of the stars is not critical. Now go back and repeat the original azimuthal adjustment. The longer you can leave the telescope tracking without significant north/south movement the better is the alignment of the polar axis. Aim for up to half an hour without significant movement of the star relative to the graticule for the azimuth adjustment and ten to fifteen minutes for the altitude adjustment. Being six hours over from the meridian the altitude adjustment is more susceptible to atmospheric refraction. Go backwards and forwards between the altitude and azimuth adjustment until you are satisfied that no further improvement is required. Once you have aligned the polar axis to your satisfaction you can then check the quality of your R.A. drive.
Your R.A. drive quality is easily checked. Do this by lining up a bright star, near to the meridian, with the illuminated graticule and looking at the east/west movement this time. Use a high magnification. You will probably find that the stellar image progressively moves backwards and forwards relative to the centre of the graticule with a time scale of four to eight minutes. If there is no such movement then you have a good drive. If you have a modern Schmidt-Cassegrain telescope then you might find that you have movement of over an arc minute which, using the electronic 'periodic error correction' built into the more recent of these telescopes, allows the drive error to be brought down to arc seconds. If the error persists at a level which is large compared with the seeing disc then you will have to guide during exposures. If you have a home made telescope and drive with a periodic error then it is up to you to either guide during exposures or correct the original fault. It might seem drastic but lapping the worm and worm wheel together with liquid metal polish and a high speed drill will cure this problem for those with the nerve to try it but you might well need to replace the worm bearings afterwards.
Matching the CCD to the telescope.
When you are confident that you have a well-aligned polar axis and a good drive you can proceed to consider which combination of optical system, f/ratio and CCD type will best suit your purposes. The aperture of the telescope you use is likely to be governed by cost. The effective focal length is up to you and/or your telescope supplier. For example a 20" (0× 5m) diameter f/4 has the same focal length, and hence the same scale in the focal plane, as an 8" (20 cm) f/10. The light gathering power and cost will be very different. To use your CCD effectively you will need to match the pixel size of your CCD to the image scale in the focal plane of the telescope. In order to use the telescope/CCD combination for imaging it is normal to arrange things so that the typical seeing disc, say 2 to 3 arc seconds, covers two pixels. This satisfies the Nyquist sampling criterion, which we need not expand upon here. However, for photometric purposes it is better if each stellar image covers more than a 2 x 2 pixel array, say a 3 x 3, 4 x 4 or even larger. Thus there is straight away an optimum relationship between the focal length of the telescope and the size of the pixels on your CCD.
Nearly all CCDs have pixels which are between 9 microns and 25 microns in size. Some CCDs have square pixels, others have rectangular. If you have the choice, opt for square pixels, but if you already have rectangular pixels then rest assured that they also can produce photometry. An easy way to calculate what focal length matches what pixel size is to remember that one arc second subtends approximately five microns with an effective focal length of one meter (about 40"). Therefore, if you typically have four arc second seeing the image will cover about a 2 x 2, 9 micron pixel array with a one meter (~40") focal length. If the focal length is two meters (~80") then four arc second images will still not fully cover a 2 x 2 array of 25 micron pixels. You will need to go up to a 2× 25 meter (~90") focal length before you cover a 2 x 2 array of these larger pixels and double that, a 4× 5 meter (~180") focal length to cover a 4 x 4 array. This criterion, that you should cover more than a 2 x 2 array of pixels on your CCD for photometric purposes, imposes quite severe restraints on the size of the field which will be obtained with all but the largest, and hence most expensive, CCDs.
It might be thought at this stage that we have arrived at a point where we can make a ready decision; where we only have to match the focal length of the telescope, the pixel size and our budget and buy the largest CCD chip with the correct sized pixels that we can afford. Unfortunately, this is not the end of the story. Prior to 1995, CCDs intended for amateur use typically had about 200,000 pixels, or less, and used a 12 bit A/D. Downloading each image took a few seconds and about five images could be stored on a typical 1× 44 Mbyte floppy disc. With the advent of Mega pixel (one million pixel) CCDs and 16 bit A/Ds it is now common for one image to take tens of seconds to download, unless a SCSI or USB system is used, and for each image to take up more storage space than one floppy can hold. The extra download time will seldom be a real problem with exposure time of tens to hundreds of seconds but image storage, and image movement between different PCs, should be taken into account when specifying ones PC. Rewritable CDs are currently available at a sensible price and rewritable DVDs are currently set to take over from CDs over the next few years. Hard drive capacities double every eight months or so and at the start of 2003 120 Gbyte capacity is readily available. Therefore, the reader needs to be aware that as attractive as it might seem to be to go for the largest CCDs that they can buy there are concomitant costs which need to be taken into account before a final decision is made.
Other things to remember when choosing your CCD.
Do not choose a chip with an anti blooming device. These can lead you into serious errors as they can mask the fact that you have saturated some of the pixels. If you already have one then use the histogram of counts versus numbers of pixels to ensue that your exposure times are short enough to avoid saturation and test the system on standard stars to discover what accuracy you can really obtain.
Choose a CCD which is cooled and temperature stabilised, not just cooled. The quality of the dark frames which you obtain is vital to the accuracy of your final photometry. It is important that the dark frames are taken at just the same temperature, as well as for the same duration, as your main exposures. You will find this almost impossible without temperature control.
Never use a CCD chip intended to produce colour images. The small filters fitted in front of the pixels are incompatible with the standard astronomical filters and as only one pixel in every three is sensitive to the colour being observed the resolution is drastically reduced.
Never use a CCD chip which is part of a chip set intended to provide blemish free images by on line processing to remove evidence of hot spots, dead pixels etc. The idea was that known chip faults could be removed on line for cosmetically appealing, commercial imaging. Improvements in CCD chip production technology mean that this is now a rare feature but some older CCD cameras were made from such chip sets and they are useless for science. Much better that you are aware of the chips defects and can work round them rather than try to work with pre-processed data where you do not even know what that processing was.
Training and testing.
Before you start to do the serious work of trying to make some scientific discoveries you will need to practice with the use of your telescope/CCD combination and software package. You would not expect to run a marathon without prior training and you should not expect to become an expert in the use of your equipment without training yourself in its idiosyncrasies. You will need to know how efficiently the telescope can be pointed at a new object and, once there, how well it tracks. If there are periodic drive errors you need to see how long you can expose without spoiling the images and if this is a negligible time then you need either to practice your guiding skills or buy and fit an autoguider. Most of the photometric reduction routines which come as part of the software package supplied with your CCD are similar but you will still need to train yourself in their use. Work out your own routines as to how you find it most useful to store and transport data. You will need a name of the object or field, the exposure time, the observatory name and/or position and some record of the sky condition, phase of moon, amount of cloud etc. Even the type of CCD and number of bits in you’re A/D might be useful as such is the rate of technological change that it is unlikely that you will still be using he same equipment ten or twenty years from now. If you do not intend to store actual images long term but only the results; and remember the new generation of megapixel CCDs can fill, or overfill, one standard floppy disc; then as well as having a header for the data file which specifies the above instrumental and other details you will need to generate a list of Julian Dates and magnitudes or D magnitudes. Note that we specify Julian Dates and not calendar dates and times. If the object of interest has a period of tens or hundreds of days then Julian Dates will suffice. If the period is hours or even minutes then Heliocentric Julian Dates will have to be used when the data is analysed. It is easier for you to store all your epochs in this form on an observation by observation or night by night basis than to place the burden for this on someone who might be wanting to use your data as part of a data set containing thousands of points some time in the future. Whatever you do, you must make it clear what system of epochs you are using.
Once you have familiarised yourself with the equipment, the software and 'data housekeeping' you can then move on to the final two tests before starting the exciting process of making new discoveries. The first of these is to do photometry on well observed star fields using only one filter in order to check how well you can reproduce the magnitudes of earlier observers. For this test we recommend that you use the V filter as it lies near to the peak sensitivity of most CCDs and V magnitudes will be available for any standard field. It is at this stage that you will become familiar with the taking and storing of both dark frames and flat fields. When it comes to reducing the data, remember that you must always remove the dark frame from the flat field before using it and from the star field before flat fielding it.
Flat fields should be obtained with the maximum density that you can get without saturating any pixels. This gives you the best signal to noise. Remember that we spent some time earlier describing how the noise varies as the inverse square root of the signal! Use the histogram of the number of pixels versus counts to ensure that you have not overexposed. Flat fields must always be taken through the same filter that you intend to use of your star field frames. If your telescope/CCD/filter assembly is totally dust proof then flat field calibration exposures can be relatively infrequent, say once a week or so. Unfortunately, if this is not the case and you live in a dusty area, and this context dust can mean pollen from crops and trees as well as dust from deserts or dry soil, then you might need to do your flat field calibrations on a nightly basis.
Dark frames are a problem. The difficulty is that by their very nature they only have a low signal, and hence a high noise. This means that the error associated with the counts in any one pixel can be percents or even tens of percents of the count itself. If you have a CCD which is only cooled and not temperature controlled then the best that you can do is to take, say, two dark frames before and after the stellar exposure and to take the mean of the four exposures. Remember that it is vital that the duration of each of the dark frames is the same as that of the main exposure. If you have a CCD which is temperature controlled then you can adopt a more efficient strategy. You can decide upon a temperature which you will always use for observing, or two temperatures if you live somewhere where summer and winter temperatures are so different that your CCD system cannot maintain one temperature year round. You will take many dark frames at that temperature and with a duration typical of your exposures. You will then take the mean of those exposures. There are two variations of this theme. The first requires a mean dark frame to be obtained for a series of typical exposure times, say 10 seconds, 20 seconds, 50 seconds and 100 seconds and then all your other exposures should use one of those times. An alternative is that the mean of many dark frames is normalised by dividing the counts in each pixel by the number of seconds for each exposure. You will then end up with counts/seconds for each pixel of your dark frame. These can then be multiplied by the length of any later exposure and this well calibrated dark frame removed from the stellar exposures.
There is a danger in this and the reader needs to be aware of the circumstances when this will not work. Some CCD camera manufacturers have designed their systems to work on telescopes where there are known to be R.A. drive periodic errors. What they do is to divide a long exposure, say ten minutes, into five, two minute sessions. At the end of each two minutes the exposure is stopped, the star re-centred and the exposure continued. The problem is that dark counts continue to accumulate during the re-centring operation and we end up with exposures where the length of time for the accumulation of the dark counts is not the same as that for the accumulation of the stellar images. We strongly recommend that you never use this type of exposure when photometry is intended.
It should go without saying that you must never try to do photometry on any image which has been processed to enhance the contrast or resolution. Pixel binning is allowed but nothing more.
Flat fields can also have a problem which we mentioned earlier and which we will mention again for emphasis. If it is your intention to use your CCD to carry out photometry of bright objects such as a planet and you have a mechanical shutter for controlling the exposure duration then you must ensure that your flat fields are of the same duration as the exposure on the planet. The problem is that the relatively slow movement of a mechanical shutter can cause the opening and closing times to be a significant fraction of the one hundredth or one fiftieth of a second exposure times often used to try to freeze the seeing when fine planetary details are being searched for. If it is your intention to concentrate on planetary work then you would be well advised to opt for a frame transfer or interline transfer CCD chip.
If all this has seemed rather complicated then you will be pleased to learn that the actual tests required for you to determine the photometric accuracy of your system are very straightforward. You will need to find a star field which has been so well observed that the magnitudes are used as standards. Which field you use will depend upon where you live and what part of the year you wish to observe. M67 is one example suitable for northern hemisphere observers. The magnitude values can be found in 'CCD Astronomy', by Christian Buil, pages 275-6 or R E Schild, 1983, Publication of the Astronomical Society of the Pacific, Vol. 95, page 1021. Reference to other suitable fields can be found in the Buil reference or in those mentioned in our earlier section on reducing your observations to a standard system.
We recommend that you start by taking nine V band exposures, complete with flat fields and dark frames of your chosen reference field. Deliberately allow the images to wander between frames so that the stellar images fall on different pixels for different exposures. Reduce each frame to the best of your ability and write out a list of D magnitudes. Refer to the list of published magnitudes and using the brightest star convert your D magnitudes to magnitudes. Note that at this stage you have not determined your colour corrections and therefore the nearer to the zenith that you can observe the better. You should now have a list of nine magnitude measurements for each of perhaps ten stars covering a magnitude range of four or five. Calculate the mean and standard error for each of the nine measures for each of the stars. Now compare the measured brightness means against the published values. You are looking for two things. How well do the magnitude means agree with the published values and how do the standard errors vary for stars progressively fainter than the brightest star?
There should be no difference between the mean of the brightest star and its published value as you used that to define the system. The standard error of the mean for this star tells you what the accuracy is of your photometry. Note that standard errors reduce as the square root of the number of measures you have taken, assuming that there are no systematic errors present. Thus if you had made four measures the standard error of the mean would have been half of the error for a single measure. You made nine measures so the standard error of a single measure will be about three times the standard error of the mean. That is if the standard error of the mean magnitude was 0× 01 mag. then the standard error for a single measure would have been about 0× 03 mag.
Next go down your list of mean magnitudes and compare them with the published values for each star. Take the difference, observed magnitude minus published value and see if you can determine a trend. You might need to plot a graph of magnitude difference versus magnitude to allow you to see any trend if it is small. You should not be able to see any trend but the scatter will go up for the fainter stars. If you can see a trend then that means that either there is a non linearity in your system or you are subtracting an incorrect value for the dark count. You will need to check your dark counts very carefully. A temperature difference of only a few degrees between the dark count frames and the stellar frames is enough to throw your measures wildly out on the fainter stars. If you cannot detect any errors and if the non-linearity is serious then your CCD is not suitable for photometry. If the trend is slight, and say the brightest three magnitudes fit a straight line, then you might be able to use the system for photometry with great care on low amplitude variables using reference stars of a very similar magnitude to the variable. Alternatively, sell the system to someone who wishes to concentrate on imaging and replace it with one designed from the start for scientific purposes.
The second check you should carry out is to see how the standard error increases with progressively fainter stars. Suppose that you have observed two stars whose brightness differs by five magnitudes, that is a factor of one hundred in linear brightness units. Because the standard error should vary as the square root of the counts the standard error for the fainter star should be ten times that for the brighter star. If the exposure is organised so that the brighter star is as near to pixel saturation as is possible and if you have a 16 bit A/D you should just about be able to compare stars over a five magnitude range. If not then you will have to use a smaller range of stellar brightnesses. Whatever the details you should eventually be able to determine whether the errors are acting as expected. If they are not then it is probable that there are sources of noise in your system which need to be tracked down and eliminated before you carry out observations. The manufacturer of your CCD should be contacted unless you are an electronic expert. Although their initial response might not be what you would hope for, eventually, it is just as much to their benefit as yours that they produce a fully debugged system.
Assuming that you do not find any problems you can then proceed to the final calibration. By this stage you should be very confident in the use of all your equipment and software. You will know what the potential accuracy of your system is and you can proceed to carry out the colour calibration of your system against standard stars as described earlier. Finally you can go back and repeat the tests on standard stars and this time re-determine your potential accuracy using the known colours of the stars as input to apply your corrections. The determination of the real accuracy of your system is important as knowing its value allows you to decide which types of observational project you can realistically undertake.
Observational Projects.
Talk to fifty different professional astronomers and ask them what they consider to be scientifically useful projects that you can carry out at your home observatory and you will probably get fifty different answers. One person's passion can all too easily be another person's boredom. At the end of the day it is your money and time which is going to be used and unless you find the project stimulating, those long, cold, lonely nights are going to take their toll and you are going to give up. We do not even understand why some people like pepperoni on their pizzas and others do not, much less why one astronomical project appeals to one person and not to another. For now, just accept that there are hundreds, possibly thousands, of scientifically worthwhile projects which you can tackle with your equipment. Your problem is to decide which ones fit in with your lifestyle, your observing site, the size and type of your telescope and the realistic accuracy of your equipment.
There is so much hype in the CCD world about how fifteenth to eighteenth magnitude objects appear above the sky background in only a few seconds that the novice user might wonder why people bother to build large telescopes any more. What those who produce the hype fail to tell you is that although it is true that you might be able to detect an eighteenth magnitude object in only a few seconds with an 8" (20 cm) telescope, there are so few counts in the image that you are not going to do anything very useful with it. You might be tempted to go round uttering the novel cry, "mine is fainter that yours", but as with so many other things in life it is not what you have got but what you can do with it that counts. At the end of the day the nature of the universe in the guise of photon statistics is going to tell you what you can and cannot do.
We can only give a rough guide to what brightness stars you can expect to observe as so much depends upon the size of the telescope, the filters used, the quality of the sky and so on. A 0× 5 metre (20") telescope on a good site records about one million (106) counts every second from a fifth magnitude star at the peak of a CCD’s response through a V filter. For illustrative purposes we will suppose that the full well capacity of your CCD is about105 and the star image covers 10 pixels. Thus a fifth magnitude star is likely to saturate your system with a one second exposure. A 25 centimetre (10") telescope will get to the same figure in four seconds and a 20 centimetre (8") in just over six seconds. A tenth magnitude star will need 100 times these exposures to get to the same figure and a fifteenth magnitude star will take 10.000 times longer. One does not obtain 10.000 or 60,000 second exposures. Working these values the other way round we can get a rough figure for how many photons there are in the image of a fifteenth magnitude star with a 100 second exposure using a 20 cm (8") telescope. The answer is about 16. Remember that these 16 counts may be spread out over 10 pixels and that the photon statistical error on 16 counts is about 25%. Publicity photographs are often taken with unfiltered CCDs which increase this number by a factor of a few. It is a measure of the usefulness of CCD technology that such an image is even detectable but you should not be fooled into thinking that you can do anything very quantitative with that number of counts.
There are far too many types of project which you can undertake for us to describe even a minute part of them. If you want to spend one hour every night that is clear then a certain type of project is possible. Alternatively, if you prefer to spend a week observing all night and every night, perhaps twice a year, then a totally different class of project is open to you. With a small CCD chip, or a partial read out of a larger chip it is possible to get an observation with every few seconds but the size of your telescope and your computers storage capacity will act as constraints. Nevertheless, at least in principle, time scales of from seconds upwards can be investigated. It is rare for CCD photometric accuracy to exceed 0× 01 magnitude but if time scales permit then binning measures taken every few seconds or minutes and taking their mean can improve on this accuracy. Remember though that the improvement in accuracy goes as the square root of the number of individual measures. If the accuracy of one measure is 0× 01 magnitude then nine measures should improve this to about 0× 003 magnitude but it will take 100 measures to improve the accuracy to 0× 001 magnitude. If the accuracy of one measure is 0× 05 magnitude then the mean of 25 exposures will be needed to obtain an accuracy of 0× 01 magnitude.
Below we give a very brief description of various types of variable and what you might look for, and why. The list is neither exhaustive nor unbiased. Other authors might well have chosen to present a different range of projects, but following the earlier analogy of walking through a forest we suggest that you follow your instincts, being only constrained by the size of your telescope and the time you have available. It is still one of the great pleasures in astronomy that the home based observer, who exercises care and attention to details in their work, is almost certain to make new discoveries of scientific value. In general these will be of minor importance but very occasionally they might transform our understanding. Your CCD, together with your time and patience, makes this possible. Good luck!
We will present the types of variable in two lists. Intrinsic variables, that is where the star truly varies in brightness, and geometric variables, that is where the variations are due to the shape of the star, eclipses and so on. Some stars can be both intrinsic and geometric variables.
Intrinsic Variables.
Supernovae. (Time scale: minutes to years, brightness variations: ~10+mags.)
The collapse, and subsequent explosion, of a massive star when it has exhausted its nuclear fuel. Possibly the favourite targets for many home based CCD users who hope to discover a supernova before it reaches maximum. Discovery of a supernova should be communicated to professional observatories at once so that spectra can be obtained. Note that supernovae are rare and you could spend your whole life looking for, and not finding, one. The success of Mark Armstrong and Tom Boles in this field is due to enormous amounts of time, preparation and organisation. Without those you might never discover a supernova. If you want to guarantee doing some science, observing previously known variables is a better project. Monitoring the light curve of a supernova after maximum and looking for variations with time scales of minutes to hours which might be evidence for the binary nature of the remnant will be more certainly productive. You must use filters and you are likely to need a large telescope but note that the emission line spectrum of a supernova means that any derived magnitudes, or D mags., will not fit well to standard systems.
Dwarf novae, also called Cataclysmic Variable. (Time scale: minutes to year, brightness variations: ~5 mags.)
A whole class of close binary stars in which one component is a compact star (white dwarf etc.). Material is transferred from the surface of the normal star to the surface of the compact star but it depends upon the strength and form of the compact star’s magnetic field as to how the binary star seems to vary in brightness. Classical dwarf nova can erupt on time scales from months to years and the eruptions are easy candidates for small telescopes. Some stars show other increases in brightness, called ‘superhumps’. Low amplitude variations on time scales of from seconds to hours can sometimes be seen and these provide clues to the binary nature of the star, the mass flow from one star to the other, hot spots on accretion discs and so on. Larger telescopes will be required to look for some of the finer detail but filters need not be used for many of these observations.
Mira and Semi Regular stars. (Time scale: hundreds of days, brightness variations: 1-3 mags.)
These are giant and supergiant stars which are near the top of the instability strip on the Hertzsprung-Russell diagram. Many have been monitored by visual observers for over a hundred years now and recent analysis of several of the light curves suggests that periodic variations might be present. The visual observations have scatter of ± 0× 5 mag. So the potential to decrease this to ± 0× 01 mag. By using CCDs could result in a dramatic improvement of our understanding of these stars. They are easy projects for users of small telescopes as many are bright and have a large amplitude. One observation in the V band every few days is a minimum requirement. The small field of view of the typical CCD might mean that the original reference stars have to be replaced by others closer to the variable.
Cepheid variables. (Time scale: tens of days, brightness variations: ~1 mag)
Cepheids are among the most famous of variables as they are intrinsically bright and their period/luminosity relation allows them to be used as distance indicators in other galaxies than our own. Currently very few double or triple mode Cepheids are known and yet these are unlikely to be intrinsically rare. Cepheid variations occur when the stars are going through a relatively rapid part of their evolution and it should be possible to detect period changes relatively easily. Two types of observation are needed. One requires an observation every night or so until several cycles have been covered. This will allow the discovery of double or triple modes of variation. This will allow those who work on stellar structure theory to refine their models for these stars. The other type of observation only requires that the maximum or minimum of a variation is observed once every year or two to allow the detection of slow period changes. We recommend that anyone interested in working on this type of project works as part of a team as the project could take many years.
B Cephei variable. (Time scale: hours, brightness variations: 0× 01 - 0× 3 mags.)
These are hot stars near to the top of the main sequence which pulsate, but there is no general agreement as to the pulsational mechanism. Their main sequence lifetimes are short and one would expect to see evidence for stellar evolution occurring from period changes. Timing maxima or minima on a regular basis would enable period changes, due either to binary motion, evolution or other causes, to be detected. The lower amplitude examples should be easy targets for producing new information.
Geometric Variables.
Wolf-Rayet stars. (Time scale: days, brightness variations: 0× 1 + mags.)
These stars are thought to be at the end of their main sequence lifetimes and appear to be losing large amounts of material. Only a few are known to be doubles and fewer yet again show eclipses. About half a dozen are certainly eclipsing binaries and it would be well worthwhile obtaining an eclipse curve for these once or twice a year. This would enable period changes to be sought which should clarify the position regarding just how much material is being lost from these stars.
Massive binary and x-ray binaries. (Time scale: days, brightness variations: 0× 01 - 0× 1 mags.)
Cygnus X – 1 is a massive x-ray binary which possibly has a black hole as a companion. At roughly 4× 5 year intervals it changes the quality of its x-ray emission. Additionally the orbital light curve, due to the rotation of the ellipsoidal shaped primary star, changes. It is not known whether this is because the star is unusual in that it possesses a compact secondary or whether other massive binary stars, that are not x-ray emitters, would show the same behaviour if observed carefully enough. One accurate observation each night would suffice but several seasons data will be needed before the results would be meaningful. The accuracy required would challenge the typical CCD and it is likely that several observations per night would have to be averaged in order to get the errors down.
Chemically peculiar A and B stars. (Time scale: days, brightness variations: 0× 1 - 0× 1+ mags.)
These are hot stars, on or near to the main sequence, which have patches on their surfaces which are grossly over (or under) abundant in some elements. As they rotate they become brighter and fainter but with different amplitudes in different colours. The amplitude versus colour data is only known for a few of these stars and they are ready candidates for observing in as many of the U, B, V, R & I bands as possible. The light variations seem to be stable over years so it does not matter how long it takes to obtain a light curve in each colour. They are very well suited to honing your observing skills.