from J BAA 110, 2, 2000 Apr

V Boötis, a semiregular variable of declining amplitude

John Greaves & J. J. Howarth

The AMPSCAN1.2 procedure is used to investigate the declining amplitude of the semiregular variable star V Boötis, using data from the BAAVSS archive.3

Introduction

V Boötis, = HD 127335 = SAO 64180 = HIP 70885 = GSC/TYC 3036 0577 I, is a semiregular variable of subtype SRa with a catalogue period4 and amplitude range of 258 days and mv 7.0 to 12.0 respectively; the spectral class is listed as M6e.4 Over the past century this star has undergone a slow decline in amplitude at its main period, behaviour which led Szatmáry et al.5 to utilise it for a practical example of wavelet analysis upon visual variable star data. The data they used came from a variety of sources and organisations, being merged prior to analysis: here the almost ninety year span of BAAVSS data is used to investigate the behaviour of this star.

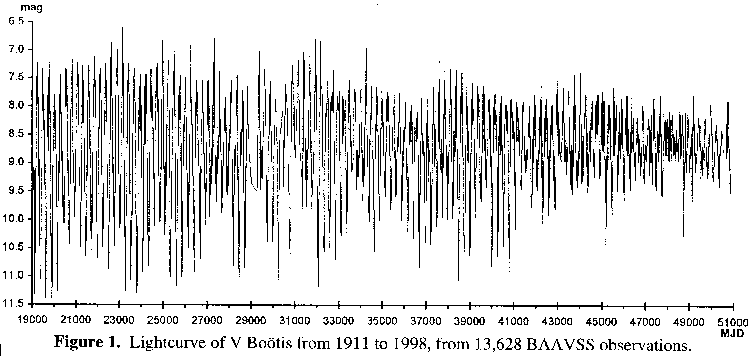
The BAAVSS data was provided in electronic form by the Section's computer archive secretary, and consisted of 13,628 positive observations that spanned the period from JD 2419000 to JD 2451000 (1911 to 1998). For processing purposes, both to lessen the computational overload and to remove the artificial weight given to better observed dates, this data was converted into 5-day means, resulting in a total of 4,866 data points. Good coverage exists throughout the full timespan of the data, although they are quite thin between ~JD 2429000 to JD 2432000 (that is, roughly for the duration of the Second World War). Figure I shows a lightcurve for this time period utilising the raw dataset of 13,628 datapoints (MJD being the Modified Julian Day, which is basically the Julian Day minus 2400000.5).

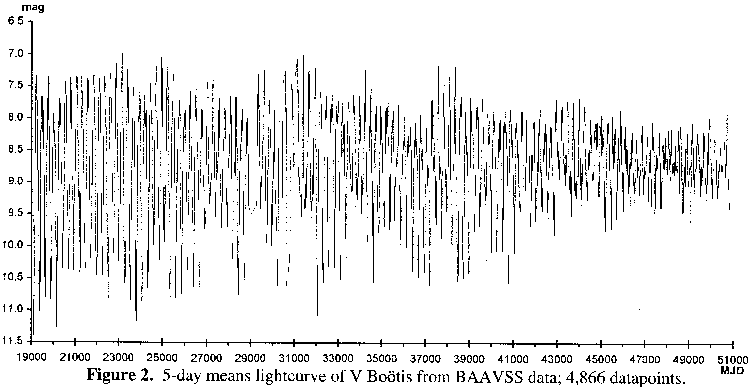
Figure 2 is a smoothed lightcurve generated using the 4,866 datapoints from the 5-day means. It can be seen that averaging the data also serves to ameliorate the effect of isolated extreme (and most likely erroneous) observations upon the lightcurve. The lightcurves also well illustrate the decline in amplitude of this variable over the timespan of the observations, despite both the mean and median magnitudes remaining near 8.70 throughout. In order to better illustrate this decline, the 5-day means were processed using the AMPSCAN method as devised by Howarth.1


Periodicity

First it was necessary to derive the period of variation for this object. The raw dataset was subjected to discrete Fourier transformation as per an algorithmic formulation by Howarth,6 frequencies being tested between the range 0.0025 to 0.025 cycles per day (400 to 40 days) at a rate of 0.00001 cycles per day per interval. The resultant amplitude spectrum, as shown by Figure 3, revealed periods of 257.8 days with a semiamplitude of 0.80 magnitudes; 151.1 days with a semiamplitude of 0.03 magnitudes; and 137.1 days with a semiamplitude of 0.03 magnitudes.

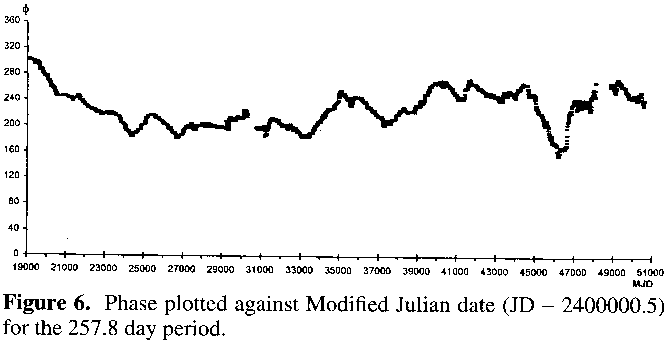
The period of 151.1 days turned out to be an alias of the 257.8 day period caused by a beat effect with an annual periodicity within the timing of the observations (ie 1/257.8 + 1/365.25 = 1/151.1), as revealed in Figure 4. Here the signal responsible for the 257.8 day peak has been removed, taking the 151.1 day peak with it. Interestingly a small cluster of peaks centred around the 259 day mark remains, which is in fact hinted at in Figure 3, and thus cannot be an alias of the 257.8 day peak. The signal at 137.1 days also remains: removal of this signal from the raw and complete dataset has no effect on the 257.8 day period or its 151.1 day alias (figure not shown). Therefore the conclusion is that, like some other semiregular variables, V Boötis' lightcurve is best represented by two periodicities: a main one of 257.8 days and a minor one of 137.1 days. From the amplitude spectrum both signals are quite stable, although the main one may show some slight variation, as indicated by the dispersion of some of the amplitude in Figures 3 and 4 to periodicities around the 259 day mark.


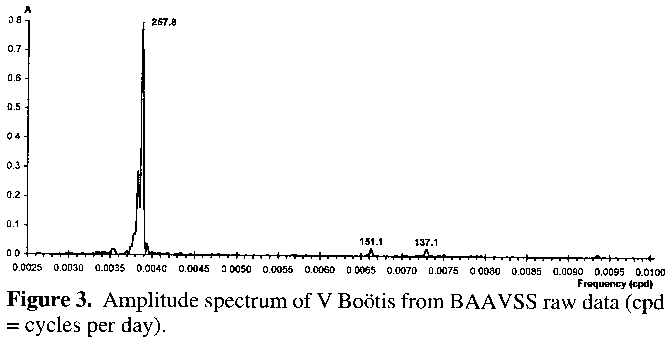
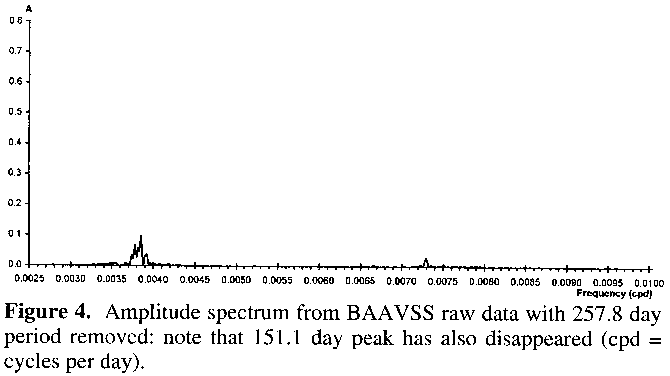
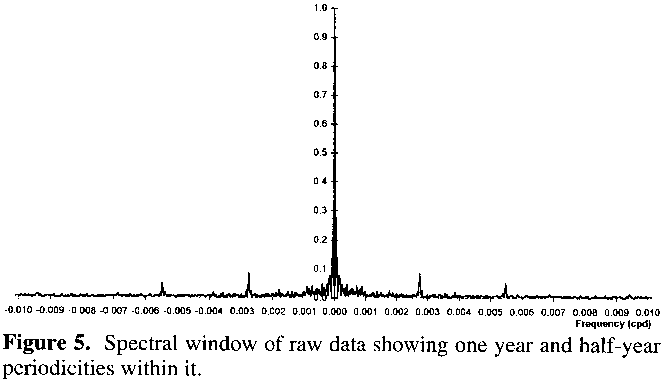
Figure 5 shows the spectral window function down to 100 days (0.01 cycles per day) taken from the raw dataset: the data was actually tested down to 50 days (0.02 cycles per day), but no further deviation from zero was found beyond 0.01 cycles per day. The figure shows that there is no inherent periodicity within the timing of the observations themselves, over and above a signal at the annual periodicity of 0.00274 cycles per day and, intriguingly, one at 0.00547 cycles per day, that is at exactly half a year. This latter could be due to a bimodal distribution in the observations, such that observers may well separate into two camps: those that observe this star all year round, and those that only observe it when it is at its best. The data was not suited to the testing of this hypothesis, however. No signal appears near the periods of 257.8 or 137.1 days, thus helping to confirm these values.

Period variation

The AMPSCAN procedure1 was used to generate plots of phase against time in step intervals of ten days. Though a little erratic due to a low amplitude and short period relative to the frequency of observation at some points in the lightcurve, the 137.1 day period appears fairly stable. Figure 6 shows the variation in phase over time for the 257.8 day period. The full range is small and deviates fairly evenly about an average phase, suggesting that it is stable about a core value. Therefore, despite some suggestion of varying periodicity, further investigation reveals that it is no more than the scatter to be expected from a semiregular star, and indeed is quite stable for such a star.

Figures 7a and 7b are phase space plots representing the evolution over time of the 137.1 and 257.8 day periods respectively. These are derived by combining the amplitude against time and phase against time data for the respective periods via the relationships x = amp x cos(phase) and y = amp x sin(phase). Plots of these values reveal period variation via transverse travel around the origin and amplitudinal variation via radial travel to or from the origin. For the 137.1 day period Figure 7a suggests that there has been little more than random fluctuation about the core value. Figure 7b reveals that after a short drift in period at the start of the dataset, the period more or less fluctuates about the core value. However, the amplitude has changed drastically.

Amplitude variation

Figure 7b reveals the decline in amplitude, the direction of evolution being denoted by open circles which depict the values at times of every thousand Julian days (i.e. the number nn represents JD 24nn000). It can be seen that there has been progressive radial travel towards lower values, i.e. that there has been a steady decline in amplitude over time.

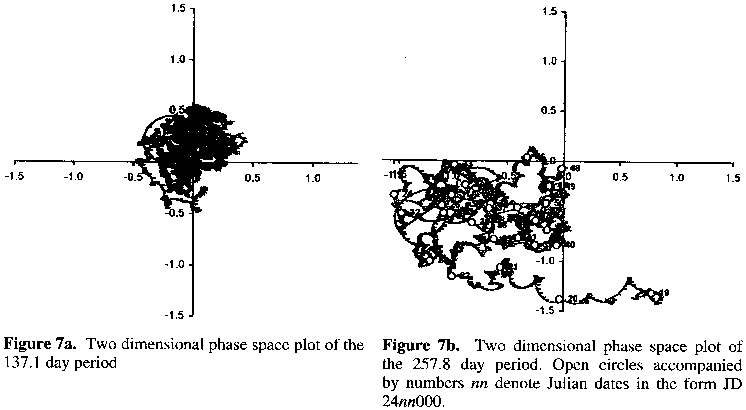
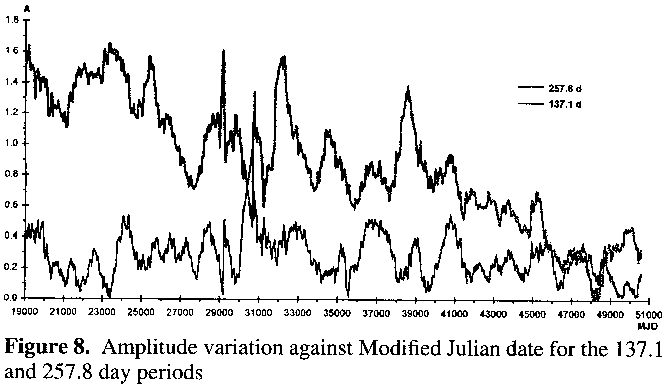
Figure 8 shows the variation of semiamplitude over time in ten day intervals for the 137.1 and 257.8 day periods. A linear fit to the semiamplitude for the 137.1 day period reveals no real trend. On the other hand, the 257.8 day period shows strong evidence for declining semiamplitude: during the early part of the data the semiamplitude averaged about 1.5 magnitudes, whereas near the end of the data that value is no more than 0.5 magnitudes (the almost complete cessation of variability around JD 2448000 is partly real but is also partly due to a paucity of data at this point, no doubt consequent upon the variable being unseasonably situated whilst near maximum).


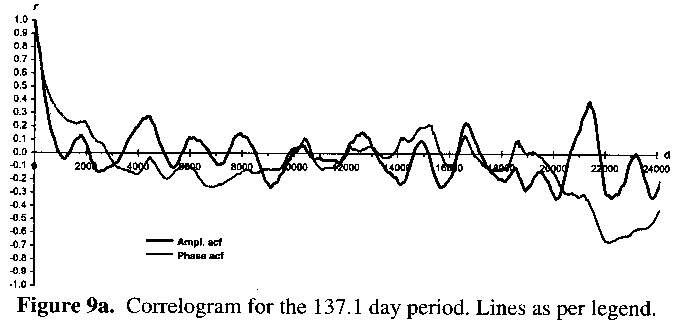
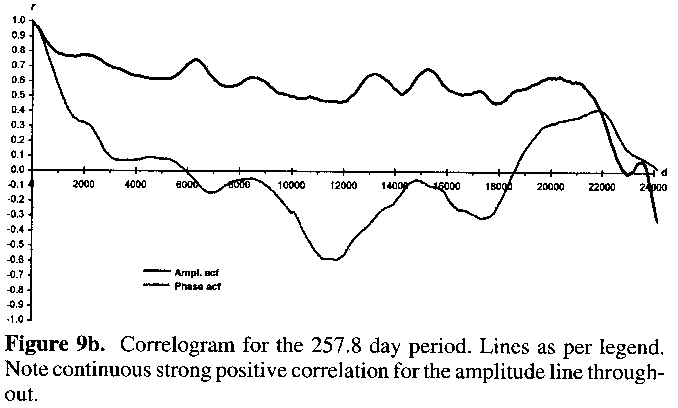
Figures 9a and 9b show the results of autocorrelation upon the data output from the AMPSCAN processing of the 5-day means data. Neither autocorrelation of phase nor amplitude reveals any high and/or consistent level of significant variation for the 137.1 day period (Figure 9a). For the 257.8 day period, however. Figure 9b reveals strong positive autocorrelation for the amplitude right up to the N/4 mark to which correlograms can be sensibly plotted (i.e. threequarters of the timespan for evenly distributed data). Throughout the timespan of the lightcurve there has been a significant tendency for any trend in amplitude variation to be followed by a like trend, which in this case is a decline in amplitude over many cycles. The autocorrelation of phase, and hence the 257.8 day period, shows little significance for concerted variation or trend thereof (as already noted).

Summary and discussion

The periodicities of V Boötis as derived from nearly ninety years of BAAVSS data were examined and found to be constant except for the usual scatter in the case of the shorter period low amplitude cycle of variation (the 137.1 day period), and constant except for scatter in the case of the longer cycle of variation (the 257.8 day period). Similarly, the amplitude of the shorter cycle, although somewhat variant, is randomly scattered within a constant range. However, the amplitude of the longer cycle has been shown to have reduced drastically and continuously (i.e. there is no evidence of stepwise jumps) over the same timespan.

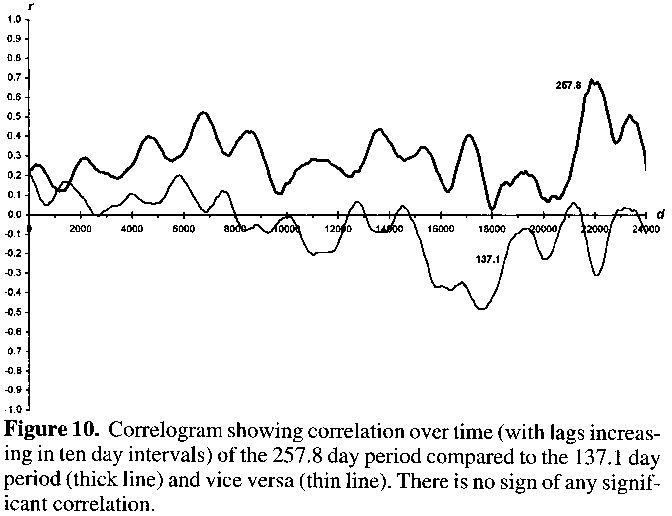
Although the period and luminosity of a star are both functions of its radius, long period variables do not necessarily need to change their periods/radii in order for their luminosity to vary. Szatmáry et al.5 gave and discounted as one suggestion a possible connection between the short and long period cycles, the shorter one 'interfering' with and thereby reducing the amplitude of the longer one. Correlating the ten day segments for the 257.8 day period's amplitude evolution against that for the 137.1 day period over time reveals no significant correlation between the two, as shown in Figure 10. Nor does any significant correlation exist for the amplitude of the 137.1 day period taken against that of the 257.8 day period (Figure 10).

The puzzle for V Boötis is to explain the reduction in amplitude about a fairly constant mean magnitude over time, whilst the period remains virtually constant. Circumstellar matter is one mechanism that can be discounted due to the lack of characteristic dips in the lightourve. Also, any such obscuration would either preferentially reduce minima, leaving maxima much the same, or if sufficient to reduce maximum luminosity, then mean magnitude would also be affected and therefore decline.

Examining the data from JD 2440000 to JD 2450000 only, reveals that V Boötis' data has a semiamplitude of around 0.46 magnitudes for the main period over that timespan, whilst the secondary period has a semiamplitude of 0.17 magnitudes. This ratio has more in common with SRb stars than with stars of type SRa, and indeed the 'recent' amplitude spectrum resembles that of SRb stars like W Tauri, It is possible that some form of damping is occurring in the ionisation zone responsible for the main 257.8 day period: quenching via core dredge up would cause metallic poisoning of the ionisation zones at the base of the radiative atmosphere, as well as potential partial disruption by causing instabilities that lead to convectional structures.

Acknowledgments

The authors would like to express their appreciation to those who have made and reported observations of V Boötis over the years, without whom this article could not exist.

References

  1. Howarth J. J., J. Brit. Astron. Assoc., 101(2), 101 (1991)
  2. Greaves J., Howarth J. J., J. Brit. Astron. Assoc., 110(3), (2000)
  3. McAdam D., BAAVSS data archive; 1998
  4. Kholopov et al.. General Catalogue of Variable Stars 4th edition, 1985-88
  5. Szatmáry K., Gal J., Kiss L. L., A&A, 308, 791 (1996)
  6. Howarth J. J., J. Brit. Astron. Assoc., 107(5), 264 (1997)